Ab initio characterization of protein molecular dynamics with AI2BMD

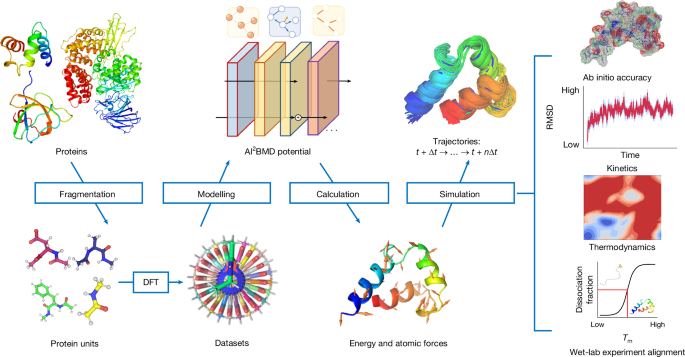
Protein fragmentation approach

Generally speaking, proteins are composed of 20 kinds of amino acid, each of which has a common main chain consisting of Cα, C, O, N and H, and a different side chain (termed the R group). A dipeptide is an amino acid capped with Ace and Nme groups at its N and C termini, respectively. As amino acids are the fundamental units of proteins, we designed the generalizable protein fragmentation approach on the basis of dipeptides and trained AI²BMD potential accordingly, which ensures the generalization ability to all proteins.

The concept of peptide fragmentation has been around for years, and previous studies have demonstrated its accuracy and efficiency to proteins^10,42. As shown in Extended Data Fig. 7a, each dipeptide consists of: all atoms of the main chain and the side chain of the amino acid; the Cα, H connected to Cα, C, O of the main chain of the previous amino acid; and the N, H connected to N, Cα and H connected to Cα of the main chain of the next amino acid. We cut the polypeptide chains with a sliding window, and thus the Ace-Nme fragments act as the overlapping regions between two successive dipeptides (Extended Data Fig. 7b). The extra hydrogens for the terminal Cα were added to dipeptides and Ace-Nme fragments, according to the C–H bond length and the direction of the bond connected to the Cα in the whole peptide chain. If the first or last amino acid was glycine, we added only one hydrogen connected to Cα according to the C–H bond length. If the latter amino acid is proline, we also added a hydrogen connected to N according to the N–H bond length where the N is connected to Cδ. Then, the limited-memory Broyden–Fletcher–Goldfarb–Shanno quasi-Newton algorithm⁴³ was applied to optimize the positions of the added hydrogens while the other parts were constrained.

We first calculated the total energy and force for all protein units by summing up the energies of dipeptides, subtracting the energies of all overlapping Ace-Nme fragments (equation (1)).

in which n is the number of amino acids or dipeptides.

The force for atoms in the same dipeptide and Ace-Nme is calculated following equation (2).

in which i denotes the atom for force calculation, m represents all of the dipeptides the atom i belongs to, n represents all of the Ace-Nme fragments the atom i belongs to, and j represents any other atom that coexists with atom i in the same dipeptide or Ace-Nme.

We further complemented the extra interactions among non-overlapped protein units. Supplementary Fig. 18 shows the extra interactions among different protein units of tetrapeptide. Two parts of interactions were not calculated. Extended Data Fig. 8a illustrates the extra interactions between the group of CH¹, C¹, O¹ and NH¹ (outlined in purple) and the last part of the tetrapeptide (also outlined in purple). Furthermore, Extended Data Fig. 8b exhibits extra interactions between the beginning part of the tetrapeptide that includes CH3⁰, C⁰, O⁰ and NH¹ (outlined in brown) and another part beginning from the second side chain to the C terminus (also outlined in brown).

Considering that the interactions in such non-overlapped regions are dominated by electrostatic force and van der Waals interactions, we used the Coulomb equation and the Lennard-Jones potential to describe them. Then, we used the corresponding parameters derived from the Amber ff19SB force field²⁰ and the distance between atoms to calculate the potential energy and atomic forces for the extra interactions (equations (3) and (4)). The selection of ff19SB was informed by its superior performance in evaluating the relative energy when compared to another widely used force field, CHARMM36 (ref. ⁴⁴), as illustrated in Supplementary Fig. 11.

in which the energy and force with the superscript ‘units’ represent the values obtained from equation (1) to equation (2), and A denotes the atom set in the corresponding unit. To avoid double counting, the sum traverses all of the atoms with the index after the current atom.

Given the protein fragmentation approach, all proteins can be converted into 21 kinds of protein unit (that is, 20 kinds of dipeptide and another Ace-Nme), which substantially reduced the number of specific types of protein unit, facilitated dataset construction and model training, contributed to exploring the whole conformational space, avoided holes in the potential energy surface, and thus improved the generalization, efficiency and robustness of the MD simulation.

Protein unit dataset

The training dataset for the AI²BMD potential was generated through the following protocols. First, the ‘Sequence’ command in the tleap module of AmberTools20 (ref. ⁴⁵) was used to generate the topology and coordinate files for the initial 20 kinds of dipeptide and Ace-Nme. Then, ϕ (that is, the dihedral of C–N–Cα–C) and ψ (that is, the dihedral of N–Cα–C–N) were two-dimensionally scanned over ranges of −180° to 175° with an interval of 5°. For the proline dipeptide, the ϕ dihedral was refined from −180° to 120° owing to its ring conformation. The rotation of the dihedral was accomplished by the ‘rotatedihedral’ command in CPPTRAJ⁴⁶. For each non-proline dipeptide, 5,184 anchors were generated. For Ace-Nme, scanning over ranges of −180° to 175° with an interval of 5° was applied on the axis of C of Ace and N of Nme resulting in 72 anchors.

Each anchor first encountered a geometry optimization (‘GO’) process to obtain a reasonable structure. The solvation model density (SMD) solvent model was used during GO. The ϕ and ψ dihedrals were also constrained the same as for anchor generation. For each anchor, the last structure of the GO process was used as the input structure for AIMD simulations. SMD was used to sample conformations by taking the solvent effect in QM into consideration. For dipeptides, 225-fs simulations were applied for each anchor, and the last 200-fs structures were extracted. Simulations of 2,025 fs were carried out for Ace-Nme, and the last 2,000 fs was extracted for each trajectory. As an explicit solvent was used during MD simulation driven by our AI²BMD potential, after AIMD simulations, we recalculated the single-point energy and forces for all extracted conformations without SMD, which were used for MLFF training.

During GO, AIMD simulations and single-point energy calculation, DFT with the M06-2X density functional with the 6-31g* basis set were used⁴⁷. This basis set and functional are generally suitable for biomolecular sampling^14,15,48,49. We set tight convergence conditions in the simulation processes, and convergence was mandatory for the next calculation step. Systems encountered a canonical sampling through velocity rescaling thermostat at 290 K (ref. ⁵⁰). Such simulations were performed by ORCA 5.0.1 (ref. ⁵¹). The charge of each system was set according to the charge for the sum of all amino acids at pH 7. The GO, AIMD simulations and single-point energy calculation took about 12,928,993 central processing unit (CPU) core hours (1,476 CPU core years) for calculation. As a result, 1,036,800 conformations were sampled and calculated at the DFT level for each kind of dipeptide and 144,000 conformations were sampled for Ace-Nme. The distributions of energy and the norm of force for each kind of protein unit are shown in Supplementary Tables 4 and 5 and Supplementary Figs. 12 and 13. The whole protein unit dataset consists of 20 million conformations that comprehensively captured the conformational space of the protein units and provided a solid guarantee for machine learning potential training and AI²BMD simulation.

ViSNet as AI²BMD potential

ViSNet is a versatile geometric deep learning model^7,52 that can predict potential energy and atomic forces, as well as various quantum chemical properties, by taking atomic coordinates and atomic numbers as inputs. As shown in Supplementary Fig. 2a, the ViSNet model is composed of an embedding block and multiple stacked ViSNet blocks, followed by an output block. The atomic number and coordinates are fed into the embedding block followed by ViSNet blocks to extract and encode geometric representations. The geometric representations are then used to predict molecular energy and force through the output block. Supplementary Fig. 2b demonstrates the ViSNet block, which consists of a message block and an update block. These blocks work together as parts of a vector scalar interactive message-passing mechanism, referred to as ViS-MP. The rich geometric information passed via ViS-MP is extracted by the runtime geometric calculation module with linear complexity. The operations in Supplementary Fig. 2b can be summarized as follows:

in which \({h}_{i}^{l}\) represents the scalar feature of node \(i\) in the lth layer, \({{\bf{v}}}_{i}^{l}\) represents the vectorized node feature and \({f}_{{ij}}\) represents the scalar edge feature between node \(i\) and node \(j\). \({\phi }_{m}^{s}\), \({\phi }_{m}^{v}\) are nonlinear message functions to transform messages from neighbours and \({\phi }_{{un}}^{s}\), \({\phi }_{{ue}}^{s}\), \({\phi }_{{un}}^{v}\) are nonlinear update functions to update the corresponding feature according to the message and geometric features. More details about runtime geometric calculation and ViS-MP can be found in ref. ⁷.

For each kind of protein unit, ViSNet was trained as an energy-conserving potential model; that is, the predicted atomic forces were derived from the negative gradients of the potential energy with respect to the atomic coordinates. We randomly split each protein unit dataset into a training set, a validation set and a test set with the ratio of 8:1:1. Hyperparameters were tuned on the validation set of the alanine dipeptide and directly applied to other protein units. Concretely, all ViSNet models trained for protein units were relatively light with only 6 hidden layers and 128 embedding dimensions for node and edge representations. To better capture geometric information, we expanded the raw three-dimensional coordinates of molecules by adapting higher-order spherical harmonics⁵³. The cutoff of the edge connection was set to 5 Å for all protein units, and the maximum number of neighbours for each atom was 32. We leveraged a combined mean squared error loss for energy and force training with the weight of 0.05 and 0.95, respectively. We adopted a learning rate of 2 × 10^−4 with 1,000 warm-up steps⁵⁴ using the AdamW optimizer⁵⁵. The learning rate decays if the validation loss stopped decreasing. The patience was set to 15 epochs, and the decay factor was set to 0.8. We also adopted an early-stopping strategy to prevent over-fitting⁵⁶. The maximum number of epochs was set to 6,000, and the early-stopping patience was 150 epochs. All models were trained on a GPU cluster with 16 NVIDIA 32G-V100 GPUs per cluster node, and the batch size was 64 or 128 per GPU according to the size of the protein units. To make the model converge better, for the training set, we subtracted the sum of atomic reference energies from the total energy and then normalized them with Z-score normalization. More details on the hyperparameters of ViSNet can be found in Supplementary Table 6.

AI²BMD simulation program

To carry out simulations with the AI²BMD potential, we designed an AI-driven MD simulation program based on the atomic simulation environment⁵⁷. Extended Data Fig. 9 illustrates the overview block diagram of the program. On program start, the initial protein structure is fed into the preprocessing module, where the solvent and ions are added, and the structure is relaxed. The entire simulation system is then sent into the MD loop, the main logic component. For each iteration in the MD loop, the protein is first decomposed into fragments by the protein fragmentation module and then partitioned by the work scheduler. The partitioning scheme is dictated by a tunable device strategy, and a user can choose to, depending on the size of the simulation system, instruct the work scheduler to maximize the utilization of all the GPUs by oversubscribing, and to reduce the memory pressure on a particular device by balancing the computation on different fragments across the GPU cards. The partitioned fragments and the solvent atoms are then asynchronously sent to different computation servers running in separate processes. This asynchronous client–server paradigm helps to alleviate a substantial limitation in the Python runtime: that only a single thread can execute Python code at a time in the same process. After the workload is distributed from the main component to the computation servers, it will be processed in parallel, and the main Python process can immediately resume processing other tasks such as persisting trajectory data, without being blocked by the servers.

Considering that cloud computing is a popular and cost-efficient way to support scientific computing workloads, we designed the simulation process to be cloud-oriented. The software configuration is fully defined with a Docker image and remains invariant across different machines, which allows us to not only effortlessly deploy the software system to the cloud, but also fine-tune the program against a fixed set of supporting libraries. As cloud-based machines may be pre-empted, and the machine-local storage is volatile during a long-time simulation, we implemented a job scheduling component that periodically persists the computation results to cloud-based storage and resumes the simulation.

System configuration in simulation

We prepared the biomolecular systems using the Amber20 package with the AMOEBA 13 force field¹⁶. The protein was first solvated in a cubic TIP3P⁵⁸ water box and then was relaxed in energy minimization cycles. Then, NaCl atoms as counterions and another 0.15 mol l^−1 buffer were added. We used classical Amber Coulombic potential-based methods to add ions. Initially, a grid of 1 Å bin size was generated, and all grids point Coulombic potentials were calculated. Then, the ions were placed on the grid where the contrast types of Coulombic potential were the highest. If an ion had a steric conflict with a solvent molecule, the ion was moved to the centre of that solvent molecule, and the latter was removed.

We adopted a hybrid calculation strategy for the simulation system; that is, the proteins were calculated by the AI²BMD potential with ab initio accuracy, whereas the AMOEBA 13 force field was used to deal with the solvent. The total energy of the system (\({E}^{{\rm{total}}}\)) is computed as the sum of the deep learning (DL) energy calculated by ViSNet (\({E}_{{\rm{DL}}}^{prot}\)) for the protein, and the energy from the MM calculation for the entire system (\({E}_{{\rm{MM}}}^{{\rm{total}}}\)). Then, to avoid double counting the energy contribution from the protein, the energy of protein atom interactions (\({E}_{{\rm{MM}}}^{{\rm{prot}}}\)) is subtracted from the total energy as shown in the following equation. Such calculations were based on the classical integrated molecular orbital + MM model implanted in the atomic simulation environment package^59,60.

Similarly, the force \({F}_{i}^{{\rm{total}}}\) for atom i is initially set as the forces from the interactions between atom i and all other atoms in the protein (\({F}_{i}^{{\rm{prot}}}\)), which is depicted in equation (4). To account for the solvent effect, an additional force was calculated between atom \(i\) and the other atoms in the system by the AMOEBA force field (the second item in equation (11)), and then the solute items were subtracted (the third item in equation (11)).

in which B represents all atoms in the entire system, and \(C\) represents the atoms in the solute. Furthermore, to calculate \({E}_{{\rm{DL}}}^{{\rm{prot}}}\) and \({F}_{{\rm{DL}}}^{{\rm{prot}}}\), we first split the protein into protein units, calculated the potential energies and atomic forces by ViSNet models and then combined all protein units by equation (3). More details about the protein fragmentation and ViSNet potential calculation can be found in the above sections. A simulation carried out under an NVE ensemble demonstrates the conserved total energy and the counterbalanced forces, thereby further substantiating the validity of subsequent sampling procedures (Supplementary Figs. 14 and 15). Furthermore, we also carried out the simulation for the same arginine dipeptide under an NVT ensemble and calculated the heat capacity by the following equation:

in which \(\langle {E}^{2}\rangle \) denotes the ensemble average of the square value of the system energy and \({\langle E\rangle }^{2}\) denotes the square value of the ensemble average of the system energy. The heat capacity values made by MM and AI²BMD are 0.052 kcal mol^−1 K^−1 and 0.053 kcal mol^−1 K^−1, which are similar and comparable to those of previous experimental studies. The subsequent simulations in this study were run in the Berendsen NVT ensembles with initial velocities randomly drawn from a Maxwell–Boltzmann distribution. The time step in this study was set to 1 fs. During the simulation, the trajectory would be written to a high-precision XYZ file.

Simulation details

In the evaluation of protein energy and force calculation, protein structures (Protein Data Bank (PDB) IDs: chignolin, 5AWL; Trp-cage, 2JOF; WW domain, 2F21; albumin-binding domain, 1PRB; PACSIN3, 6F55; SSO0941, 5VFK; APC, 5IZA; polyphosphate kinase, 1XDO; aminopeptidase N, 4XN9) were solvated in a generalized Born implicit solvent model. The alteration on the WW domain follows the GTT mutation in the previous study⁴, and the first five flexible residues in the albumin-binding domain were removed. The Amber program makeCHIR_RST was used to create chiral restraint files during replica-exchange molecular dynamics (REMD) simulation to preserve chiral properties at high temperatures. After 1,000 steps of minimization, equilibration runs of 200 ps were conducted at temperatures ranging from 300 K to 1,000 K with a stride of 100 K. The final equilibrated structures were used for REMD simulations at the corresponding temperatures. During the simulation, each replica ran for 2 ps before exchanging with neighbouring temperatures and 5,000 exchanges occurred in each production run. REMD trajectories were divided into three states according to the Cα RMSD against the crystal structure. Specifically, for chignolin, the folding structures have an RMSD of 0–2.5 Å, the intermediate structures have an RMSD of 2.5–7.5 Å, and the unfolding structures have an RMSD of more than 7.5 Å. For other proteins, the ranges of the three states are 0–5 Å, 5–15 Å and >15 Å. Then, folding and unfolding states were further divided into 5 clusters, and the intermediate structures were divided into 10 clusters via the CPPTRAJ ‘cluster’ program. We picked the structures of each cluster centre, accumulating 20 initial structures in total. Finally, each initial structure was solvated in a 5-Å TIP3P water box and encountered 10 steps of 1-fs AI²BMD simulation. Simulations were carried out under an NVT ensemble. The simulation temperature (300 K) was controlled by a Berendsen thermostat and τ was 10 fs. The reference energy and force of the corresponding structures were calculated at the M06-2X–6-31g* level. MM energy and force were calculated by the ff19SB force field.

For sampling on Ace-N-Nme, we constructed the system using the ‘sequence’ command in tleap, and then applied a 10-ns REMD simulation, identical to the one used for protein sampling. From this, we extracted 50 representative structures using the CPPTRAJ ‘cluster’ program. We then conducted 10-ps simulations for each initial structure using AI²BMD with AMOEBA polarizable embedding, resulting in a cumulative sampling time of 500 ps. We also implemented 10-ps simulations using QM–MM with AMOEBA polarizable embedding and MM with Amber ff19SB on these conformations. Each simulation incorporated a water box of 5 Å. We then examined each snapshot during the simulations to locate any water molecules that formed a hydrogen bond with the main chain or side chain (criteria: frequency >90%, donor atom distance <3.5 Å, O–H–O angle >150°). Subsequently, we delineated the distribution of donor atom distances. Following the formation of one hydrogen bond, we isolated the water and Ace-N-Nme molecules and incrementally pulled the water from 2.5 Å to 4.0 Å to form 150 structures. Finally, we carried out single-point energy evaluation on the system of the water molecule and the dipeptide by QM at the M06-2X–6-31g* level, AI²BMD with AMOEBA solvent and MM with ff19SB.

For AI²BMD simulation on dipeptides, we first generated the conformations of the dipeptides through the ‘sequence’ command in tleap. Then, the dipeptides were solvated in a 5-Å TIP3P water box, and we ran two repetitive 500-ns classical MD simulations under the ff19SB force field for sufficient sampling. k-means clustering was then applied, and 50 representative structures were picked up. Starting from the representative structures, we carried out 10-ns AI²BMD simulation for the negatively charged protein unit Ace-E-Nme, the positively charged Ace-R-Nme, Ace-F-Nme with a benzene ring in the side chain and Ace-S-Nme with a smaller side chain solvated by a 10-Å water box under an NVT ensemble. Furthermore, for J coupling analysis, 2 independent runs of 1-ns AI²BMD simulations were used, and 10,000 snapshots were saved. Then, ϕ values were estimated from each snapshot. The ³J(H_N, H_α) coupling value was calculated through equation (13).

For AI²BMD simulation on chignolin, we first aligned the structures in a 106-μs comprehensively sampled trajectory to the initial structure. Then, time-lagged independent component analysis was used on raw atom coordinates for projecting the free-energy landscape to a six-dimensional super surface⁶¹. On the basis of minibatch k-means algorithm, we clustered all conformations and then picked up 60 folded and unfolded structures as the representative structures. Then for each structure, we ran 10-ns AI²BMD and 10-ns MM simulations.

In the Ramachandran plot, ϕ is the dihedral angle determined by C_n−1, N_n, Cα_n and C_n, and ψ is the dihedral angle determined by N_n, Cα_n, C_n and N_n+1. The subscript represents the index of a residue in a protein. The energy was estimated according to a Boltzmann distribution based on the density of points in each bin. This estimation was carried out using the potential of mean force. ϕ and ψ were set as two reaction coordinates (x, y). The potential of mean force values were calculated using equation (14).

in which \({k}_{{\rm{B}}}\) represents the Boltzmann constant, T is the temperature of systems (300 K) and \(g(x,{y})\) represents the normalized joint probability distribution. The free-energy value presented in the plot represents a relative energy value, computed by deducting the minimum free-energy value from the observed value. The Q score was calculated through equation (15) (ref. ²³).

Native contacts were defined as any pairs of heavy atoms of two residues separated by at least three residues and the distance of which is smaller than 4.5 Å in the native conformation. Equation (14) sums N pairs of native contacts in the crystal structure; \({r}_{{ij}}^{0}\) is the distance between heavy atom i and atom j of native contacts in the crystal structure, \({r}_{{ij}}(X)\) is the distance between atom i and atom j in the conformation X. The thresholds of Q values for folded and unfolded structures were set to >0.82 and <0.03, respectively²³.

For free-energy estimation for fast-folding proteins, we first evenly sampled 100,000 points in the simulation trajectories of ref. ⁴. Folded and unfolded states were classified by the same thresholds of Q values in the previous study²³. Structures in the folded state were clustered into 10 clusters. The RMSD values were calculated on the basis of Cα coordinates according to the ‘rmsd’ method in MDTraj. ΔG, the free energy for the folding process, was calculated according to the ratio between the folded and unfolded structures. Using the re-evaluated energy for each conformation, we determined the folding enthalpy and the heat capacity change for protein folding. The melting temperature was extrapolated from the calculated ΔG, folding enthalpy and the heat capacity change.

For the calculation of changes in enthalpy and heat capacity during protein folding and unfolding, 110-residue barnase (PDB: 1A2P) and 84-residue CI2 (PDB: 2CI2) were selected for evaluation with enthalpy and heat capacity values measured by differential scanning calorimetry and spectroscopy^36,37. For each protein, besides the folded structure derived from PDB, 20 unfolded structures were also generated for simulation. Following the previous study³⁵, each conformation was explicitly solvated by a 10-Å water box. For barnase, 20 parallel simulations starting from the folded structure and 20 simulations starting from the unfolded structures were performed by GROMACS 2018 with the CHARMM36 force field at pH 4.1 and at temperatures of 295 K, 315 K and 335 K. The same settings were applied for CI2, except the simulations were carried out at pH 6.3 and temperatures of 335 K, 350 K and 365 K. Each system configuration above was conducted 2-ns simulation under an NPT ensemble. Potential energy values of conformations sampled from simulations were calculated by AI²BMD. The enthalpy change following thermal unfolding (ΔH) was calculated as the difference between the averaged enthalpy of the unfolded ensemble and that of the folded ensemble. We then conducted linear regression to determine the change in heat capacity (ΔC_p) from the slope, as well as the enthalpy change at the melting temperature. Additionally, we also estimated the folding free energy using the Gibbs−Helmholtz equation.

In the pK_a determination using thermodynamics integration, we initially reweighted for all data points in the simulation trajectories provided by The Amber Project (https://ambermd.org/tutorials/advanced/tutorial6/index.php). Subsequently, we focused on the trajectories’ converged sections, selecting 2,500 data points per window for the dipeptide and 500 data points per window for thioredoxin to calculate the mean energy values. ΔG was computed using the integral:

in which w_λ represents the window width, U denotes the internal energy, and λ specifies the sampling window. This approach encapsulates the free-energy variation across different protonation states, facilitating the accurate computation of the pK_a value.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.