Datasets of forest fire, land surface characteristics, surface energy and water fluxes
Fire events
Information on individual fire events was obtained from the GFA database51 for the period of 2003â2016. This dataset was constructed using the daily 500âm MODIS Collection 6 MCD64A1 burnt area product52. The GFA dataset has been validated against fire event data derived using medium-resolution (30âm) satellite images and forestry agency statistics for the continental USA51. Fire size, fire duration and fire spread rate are provided in the GFA and have been reported to be largely in agreement with the validation data, although with a slight underestimation51. The GFA has a minimum fire size of 0.25âkm2 but to avoid observational uncertainties associated with small fire patches, only fires larger than 1âkm2 (roughly four burnt pixels in the 500âm MODIS dataset) were included in our analysis, ultimately leaving 84,510 fires.
A global, systematic evaluation of the MCD64A1 burnt area data showed that over the boreal forest, the product has an omission error of 27%, which is roughly compensated for by a commission error of 24%, but in temperate forest, it omits a large proportion of fires53. Additional studies show that over boreal Eurasia and over Canada and Alaska, MCD64A1 underestimated the burnt area by about 20% (refs. 21,54). Given that our research domain (40°âNâ70°âN) is mostly covered by boreal forest and that our focus is on how postfire biogeophysical processes respond to changes in fire size rather than changes in burnt area, the mapping accuracy of MCD64A1 was considered acceptable. Moreover, to the best of our knowledge, the GFA is the only openly available fire patch dataset spanning multiple years and covering the entire spatial domain of our research area, simultaneously providing information on fire duration and fire spread rateâall these features make it a suitable product for this study. The spread rate for a given fire patch was calculated as the mean value of the spread rates for all the underlying 500âm burnt pixels of a given patch51.
Nonetheless, the omission of the burnt area by MCD61A1 in boreal regions probably leads to the underestimation of fire size, which is confirmed by comparing the GFA with three regional fire patch datasets of higher quality than the GFA for Canadian and Alaskan boreal forests (Supplementary Note 1). The first two regional datasets cover both Canadian and Alaskan forests and were generated by the Arctic-Boreal Vulnerability Experiment (ABoVE) project by combining fire perimeter information from the Alaskan Interagency Coordination Center and Natural Resources Canada with either burn severity information derived from Landsat images (ABoVE-Landsat) or with the burn date information from the MODIS MCD14ML active fire product (ABoVE-MODIS). The third dataset covers Alaska only and was obtained from the Monitoring Trends in Burn Severity (MTBS) project, which is based on Landsat images. These three datasets are not subject to the omission/commission errors associated with MCD64A1. The major conclusion of this studyâthat the forest fire size amplifies postfire surface warmingâwas tested using these high-quality fire patch datasets and found to be robust (Supplementary Note 1).
The GFA is also known to erroneously divide a single fire patch spanning two MODIS tiles (each tile covering a 10°âÃâ10° region) into two patches. However, our analysis revealed that fire patches subject to this error accounted for negligible percentages of the total number of fires and total burnt area (Supplementary Note 5). The analysis in this study was complemented by a comparison of the results based on the GFA with those based on another MCD64A1-based fire patch dataset (GlobFire), which is free of tiling error. This comparison showed consistent results derived using the two datasets, confirming the negligible influence of the tiling error in the GFA on our key findings (Supplementary Note 5).
Fire intensity
FRP for 2003â2016 was obtained from the MCD14ML active fire product55, which contains the geographical coordinates of individual pixels with a nominal resolution of 1âkm, where ongoing active burning is detected. FRP denotes the radiative energy emitted per unit time during burning over the area of the observed active fire pixel and has been widely used as a proxy for fire intensity56. An active fire pixel is considered to belong to a fire event if its centre is located in a 500âm buffer zone of the event perimeter and if its detection date lies between the start and end dates of the concerned fire event.
Although an active fire pixel has a nominal area of 1âkm2, its actual area increases as the satellite sensor view moves away from the nadir. Hence, the view angle information was used to calculate the actual area of a given active fire pixel, over which the given FRP was measured. More specifically, the area of an active fire pixel was calculated as the product of the along-scan (image-scanning direction) pixel length and the along-track (satellite movement direction) pixel length, as described previously57,58. The mean FRP per area (MWâkmâ2) of a fire event was finally obtained by dividing the total FRP of all the active fire pixels in a fire patch by their total area.
Forest type
The spatial distribution of forest type was derived from the 300âm global land cover maps for 2002â2015 produced by the European Space Agency (ESA) Climate Change Initiative (CCI) land cover project. To match the resolution of the GFA dataset, the 300âm land cover maps were resampled to 500âm resolution using the nearest-neighbour method. All the land cover types belonging to the âtree coverâ type in the original classification system were treated as a forest. On the basis of the resampled 500âm ESA CCI land cover data, the annual proportions of forest area to total land area (including all the land cover types except for water bodies) were calculated for each 2° grid cell for 2003â2016, followed by the calculation of the multiannual mean proportion (shown as colour opacity in Fig. 1e). Four types of forest were distinguished: ENF, DNF, DBF and MF (a mixture of broadleaf and needleleaf). The relative proportions of ENF, DNF and MFâ+âDBF to forest area over each 2° grid cell were calculated to show the spatial pattern of forest type composition across the study domain (Fig. 1e).
The dominant forest type for each fire event was determined as follows: for an event to be classified as dominated by ENF, DNF or DBF, at least 50% of its 500âm burnt area pixels must be covered by that specific forest type. If the proportion of any forest type is less than 50%, but the total area of all the forest types covers more than 50% of fire event area, then the event is classified as MF.
Forest mortality
The Global Forest Change dataset (version 1.6) was used to obtain forest mortality following fire. This dataset provides annual forest loss information derived using Landsat data at a 30âm resolution for 2003â2018 (ref. 58). Ratios of the number of 30âm Landsat pixels undergoing forest loss to the total number of 30âm forest pixels (defined as those with a tree cover of >15% for 2000, also provided in the Global Forest Change dataset) of each individual 500âm burnt pixel were calculated, and were further averaged to obtain the forest mortality for each fire event.
Extended tree mortality, occurring up to ten years after fire, has been reported in field observations from temperate and boreal forest biomes59,60,61, but most mortality events occur in the first three years after fire. Satellite-based forest mortality derivation must account for such extended mortality events. However, salvage logging might lead to the false attribution of forest loss to fires. To balance the omission error due to neglecting long-term tree mortality and the commission error of potentially including salvage logging events, fire-induced forest mortality was defined as including forest deaths in the year of fire and one year after fire (a two-year time window). Although a three-year time window, that is, including forest deaths up to two years after fire and in the year of fire, was used in a previous study8, we found using three- or two-year time windows yielded negligible differences in the derived forest mortality, but accounting for forest loss only in the year of fire occurrence reduced the estimated mortality by a half (Supplementary Figs. 6 and 7). Nonetheless, all the mortality rates derived using the time windows of different lengths significantly increase with fire size (Supplementary Figs. 6 and 7).
LAI
The MODIS Collection 6 MOD15A2H LAI product with a 500âm spatial resolution and an 8-day time step for 2002â2017 was used. All the observations available at the 8-day time step were used, with no gap filling for the missing data. The quality of this dataset has previously been assessed using ground-based LAI measurements and by comparison with other LAI products62,63.
Land surface radiometric temperature
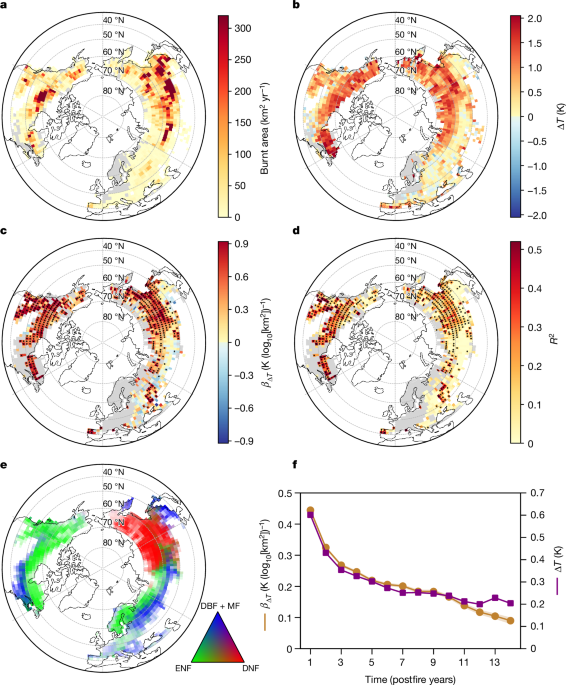
The 8-day MOD11A2 Collection 6 daytime (10:30) and night-time (22:30) land surface radiometric temperature (LST) product for 2002â2017 was used. This product was derived from the MODIS sensor onboard the Terra satellite and has a spatial resolution of 1âkm. Only the available observations with a reported error less than 2âK were used, with no gap filling for the missing data. The dataset was resampled to 500âm resolution using the nearest-neighbour method to match the 500âm spatial resolution of the MCD64A1 burnt area data underlying the GFA fire event dataset. The observed daytime and night-time surface temperatures were averaged to obtain daily surface temperature (the equivalents of Fig. 1bâd but for daytime and night-time LST are shown in Supplementary Fig. 28).
Surface albedo
The MODIS Collection 6 MCD43A3 surface albedo product at a 500âm resolution for 2002â2017 was used. The 16-day temporal resolution of this dataset provides an appropriate trade-off between the availability of sufficient angular samples and the temporal stability of the surface albedo64,65. All the observations available at the 16-day time step were used, with no gap filling for the missing data. White-sky albedo, derived by integrating a bidirectional reflectance distribution function over both incoming and outgoing hemispheres and independent of illumination or atmospheric conditions22, was used in this study. Specifically, the white-sky albedo for the total shortwave spectrum (0.3â5.0âμm) was used.
Shortwave radiation
Incoming shortwave solar radiation was used to calculate changes in absorbed shortwave radiation by the land surface due to postfire changes in surface albedo. Monthly gridded shortwave radiation (SWin) at 1° spatial resolution for 2003â2016 from the global surface radiative flux data of CERES_EBAF_Edition4.1 was used. This dataset was obtained from the NASA Clouds and the Earthâs Radiant Energy System (CERES). The coarse resolution of the shortwave radiation data is consistent with our research aim of examining the local biogeophysical effects of fires while ignoring fire-induced cloud-regime changes and their associated effects on incoming shortwave radiation.
Ecosystem ET
The MODIS Collection 6 MOD16A2 ET product (2002â2017) with a 500âm resolution and an 8-day time step was used. This product is based on the PenmanâMonteith equation and uses meteorological reanalysis data (for example, surface air temperature, surface air pressure, humidity, radiation and fraction of photosynthetically active radiation) and land surface characteristics (for example, land cover, LAI and albedo) from MODIS products as inputs66. ET was defined as the total water loss to the atmosphere as an integration of soil evaporation, wet canopy evaporation and plant transpiration66.
Snow cover
The daily MODIS Collection 6 MOD10A1 snow cover product at a 500âm resolution for 2004â2017 was used to explore the effect of snow on postfire biogeophysical changes in winter (Supplementary Note 2). Snow cover was detected using the normalized difference snow index. All the observations available at the daily time step were used, with no gap filling for the missing data.
Analysis of postfire biogeophysical responses to fire size
This study quantified the impacts of forest fire on biogeophysical variables staring from 1 year to up to 14 years after fire, in summer (JuneâAugust), winter (DecemberâFebruary) and on annual timescales. The mean values for summer, winter and the annual value of these variables were first calculated by averaging the observations with the respective time steps of different variables, over the corresponding time lengths of summer, winter and all year round (annual), followed by the application of the space-and-time approach to derive fire impacts (described below).
Quantifying postfire biogeophysical responses
Fire impacts on various biogeophysical variables (namely, LAI, LST, surface albedo and ET) were quantified as the change in variable the year after fire compared with the year before fire. The MCD64A1 burnt area data underlying the GFA dataset were used to derive postfire biogeophysical impacts for each 500âm burnt pixel. A space-and-time approach was used to isolate fire impacts by subtracting the background variation from the gross change over time. This method has been demonstrated to be effective in quantifying changes in land surface temperature due to fire disturbance or forest cover change67,68,69.
Taking LST as an example, the space-and-time approach assumes that for a given burnt pixel, the gross change in LST between the years after and before fire (ÎTgross) is the sum of the LST change induced by fire (ÎT) and a residual change (ÎTres) caused by interannual large-scale climate variations (equation (1)):
$$\Delta {T}_{{\rm{gross}}}=\Delta T+\Delta {T}_{{\rm{res}}}.$$
(1)
It, therefore, follows that
$$\Delta T=\Delta {T}_{{\rm{gross}}}-\Delta {T}_{{\rm{res}}}.$$
(2)
In equation (2), ÎTgross can be readily obtained for a burnt pixel, and ÎTres can be approximated as the mean ÎTgross of the unburnt control pixels and neighbouring pixels, and is considered comparable to the burnt pixel. The identification of an unburnt control pixel requires the following four conditions to be satisfied.
First, the candidate control pixel needs to be in an area of 50âÃâ25âkm2 (over a grid of longitudeâÃâlatitude, corresponding approximately to 100âÃâ50âpixel2 in the 500âm MODIS dataset) surrounding the target burnt pixel. Second, the candidate control pixel must not have been burnt during the same year as the target burnt pixel nor in the following year. Third, it must be covered with the same forest type as the burnt pixel. Fourth, to exclude potential impacts on ÎTres by disturbances other than fire, for example, harvest or wind damage, the cumulative tree cover loss (as a percentage) of the candidate control pixel during the year when the target pixel burnt and the following year cannot exceed 20%.
The size of the local window (50âÃâ25âkm2) used above was determined following several previous studies that used a similar approach to quantify surface radiometric temperature change following forest cover change or fire disturbance (for example, a window of 50âÃâ50âkm2 was used in ref. 68; a window of 50âÃâ28âkm2 was used in ref. 8; and a window of 25âÃâ25âkm2 was used in ref. 70). Alternative search windows of 25âÃâ25âkm2 and 50âÃâ50âkm2 were also used to quantify the linear relationship between postfire summer surface warming and log10[fire size]. The derived slopes were almost identical for the different window sizes (Supplementary Fig. 8), indicating that our results are robust across a fourfold change in search window size.
Fire-induced LST change at fire event level is defined as the average of the ÎT values of all the burnt pixels for a given event. Fire effects on LAI (ÎLAI), albedo (Îα) and ET (ÎET) were calculated following a similar approach.
Resolving changes in land surface energy fluxes after fire
Changes in surface radiometric temperature following fire are the outcome of changes in the surface energy balance, which can be expressed as
$$\Delta {R}_{{\rm{n}}}=\Delta {{\rm{SW}}}_{{\rm{in}}}-\Delta {{\rm{SW}}}_{{\rm{out}}}+\Delta {{\rm{LW}}}_{{\rm{in}}}-\Delta {{\rm{LW}}}_{{\rm{out}}}=\Delta {\rm{LE}}+\Delta (H+G),$$
(3)
where ÎRn is the change in net radiation that measures the surface radiative impact of fires; ÎSWin, ÎSWout, ÎLWin and ÎLWout are changes in the incoming and outgoing shortwave and longwave radiation, respectively. ÎLE and Î(Hâ+âG) are changes in latent heat flux and changes in the sum of sensible heat flux and ground heat flux, respectively. The change in the energy storage of the land surface was not included.
This analysis considered only local effects on surface temperature due to forest fires by comparing burnt pixels with their surrounding unburnt pixels. Hence, feedback effects such as fire-induced cloud-regime changes (which mainly occur beyond local scales) were not considered. This simplification leads to the assumption that no changes occurred in SWin or LWin due to fire, and therefore, the change in net radiation can be expressed as
$$\Delta {R}_{{\rm{n}}}=-\Delta {{\rm{SW}}}_{{\rm{out}}}-\Delta {{\rm{LW}}}_{{\rm{out}}}.$$
(4)
ÎSWout can be derived by combining the surface albedo change (Îα) and SWin:
$$\Delta {{\rm{SW}}}_{{\rm{out}}}=\Delta \alpha \times {{\rm{SW}}}_{{\rm{in}}}.$$
(5)
As fire influences surface temperature, outgoing longwave radiation also changes. LWout can be calculated from the surface radiometric temperature (T) and emissivity (ε) using the StefanâBoltzmann law:
$${{\rm{LW}}}_{{\rm{out}}}=\varepsilon \sigma {T}^{4},$$
(6)
where Ï is the StefanâBoltzmann constant (5.67âÃâ10â8âWâmâ2âKâ4).
The MOD11C3 product provides surface emissivity estimates for the middle and thermal infrared bands that can be used to obtain ε using an empirical equation71:
$$\varepsilon =0.2122{\varepsilon }_{29}+0.3859{\varepsilon }_{31}+0.4029{\varepsilon }_{32},$$
(7)
where ε29, ε31 and ε32 represent the surface emissivity for MODIS bands 29 (8,400â8,700ânm), 31 (10,780â11,280ânm) and 32 (11,770â12,270ânm), respectively.
ÎLWout can then be approximated by the first-order differential of equation (6). But given its strong nonlinearity, a distinction is made between changes in daytime and night-time LST:
$$\Delta {{\rm{LW}}}_{{\rm{out}}}=\frac{1}{2}\sigma [({T}_{{\rm{day}}}^{4}\Delta \varepsilon +4\varepsilon {T}_{{\rm{day}}}^{3}\Delta {T}_{{\rm{day}}})+({T}_{{\rm{night}}}^{4}\Delta \varepsilon +4\varepsilon {T}_{{\rm{night}}}^{3}\Delta {T}_{{\rm{night}}})],$$
(8)
where ÎTday, ÎTnight and Îε refer to postfire changes in daytime and night-time surface temperatures and surface emissivity, respectively. A single value of Îε was used for both daytime and night-time because only a daily value is provided in the MOD11C3 product.
The latent heat flux (LE; unit: Wâmâ2) can be derived from ET (unit: mmâdayâ1) as
$${\rm{LE}}=\rho {L}_{{\rm{v}}}\times {\rm{ET}},$$
(9)
where Ï is the density of water (a constant value of 1.0âÃâ103âkgâmâ3 was used) and Lv is the latent heat of vapourization for water (a constant value of 2.5âÃâ106âJâkgâ1 was used). The conversion coefficient between ET (mmâdayâ1) and LE (Wâmâ2) can be calculated using equation (9) as 28.94âWâmâ2â(mmâdayâ1)â1. Therefore, the change in latent heat flux (ÎLE) is given by
$$\Delta {\rm{LE}}=\Delta {\rm{ET}}\times 28.94\,{\rm{W}}\,{{\rm{m}}}^{-2}\,{({{\rm{mm\; day}}}^{-1})}^{-1},$$
(10)
Finally, changes in the sum of the sensible heat flux and ground heat flux can be derived as
$$\Delta (H+G)=-\Delta {{\rm{SW}}}_{{\rm{out}}}-\Delta {{\rm{LW}}}_{{\rm{out}}}-\Delta {\rm{LE}}.$$
(11)
Note that all the terms on the right side of the above equation have their associated observation errors that we have not explicitly addressed here, which are then included in the term on the left side.
Linear relationships between biogeophysical changes and fire size
Simple linear regressions of the form yâ=âαâ+âβâÃâlog10[fire size], between postfire biogeophysical responses (ÎLAI, Îα, ÎET and ÎLST) and changes in land surface energy fluxes and fire size, were conducted to detect the impact of fire size on postfire biogeophysical processes. The derived regression slope of fire size is defined as fire size sensitivity (the β value). Following the observation that fire size fits a log-normal distribution in different ecosystems around the globe72, log10[fire size] was used as the independent variable. Such a logarithmic transformation of fire size or burnt area is widely used in forest fire studies17,30,73. The minimum fire size required for a fire event to be included in the regression was set at 1âkm2 (that is, four 500âm MODIS burnt pixels), to remove possible observational uncertainties associated with small fire patches.
Furthermore, simple linear regressions between fire size and fire behaviour variables (fire duration and fire spread rate), and between fire intensity, forest mortality and fire size, were also performed to examine changes in fire behaviour and fire severity with fire size.
For all the above variables, linear regressions with log10[fire size] were fitted in each 2° cell with a minimum of 10 fires to display the spatial pattern of the β value and the possible influence of forest type (Figs. 1c,d and 2, Extended Data Fig. 6 and Supplementary Fig. 7). Moreover, we applied a more rigorous field significance test corrected for the FDR (αFDRâ=â0.1) following ref. 74. For observations showing moderate to strong spatial autocorrelation, the global significance level (αglobalâ=â0.05) is about half that of αFDR (ref. 74). The test corrected for FDR was carried out using the stats.multitest module in the statsmodels Python package based on the BenjaminiâHochberg method. Pixels with locally significant regressions (Pâ<â0.05) and those passing the field significance test corrected for FDR are shown in our results.
For changes in LST and land surface energy fluxes after fire, a single linear regression with fire size, including all fires in the study domain, was also performed to obtain the domain-wide β values (Fig. 1f and Extended Data Fig. 4). A multiple linear regression model with interaction terms between fire size and forest type was used to test whether significant differences exist in the β values among different forest types (Fig. 3). The forest type was treated as a categorical variable with its values being ENF, DNF, MF or DBF. A two-tailed t-test for the interaction term was used to examine whether significant differences existed in the regression slopes (namely, β values) among the forest types (Pâ<â0.05). The values of the determination coefficient (R2) of multiple linear regressions are as follows: ÎLAIâ=â0.23, ÎETâ=â0.12, Îαâ=â0.20 and ÎTâ=â0.31.
Multiple linear regression models using postfire change in LST as the dependent variable, and log10[fire size], ÎLAI, fire intensity (FRP) and forest mortality as independent variables, were conducted both in each 2° grid cell and by including all fires in the study domain, to examine the direct size impact after accounting for co-varying fire behaviour variables with size (Supplementary Note 4.1 and Supplementary Fig. 23a).
Fire vulnerability was defined in terms of the mean values of postfire changes in LAI and LST, and forest mortality of all fires. The Tukeyâs honest significant difference test for multiple comparisons was used to test significant difference in fire vulnerability among forest types (Fig. 3).
We examine the impact of the edge effect, where a linear relationship between postfire surface warming and fire size would be potentially driven by a decreasing fraction of the patch area located near its edge as its size increases. This analysis shows that the reported enhanced postfire surface warming (and other biogeophysical variables) with fire size is unlikely to be an artefact of the edge effect (Supplementary Note 6).
Long-term biogeophysical responses after fire and their changes with fire size
The space-and-time method used to quantify biogeophysical and surface energy flux changes one year after fire (that is, ÎT, ÎET, Îα and changes in surface energy fluxes) and the linear regressions of these variables with log10[fire size], as described above, were extended for up to 14âyears after fireâthe longest period with records available. Control pixels that were used to derive the residual changes (namely, ÎΤres in equation (2) and for other similar variables) were limited to neighbouring pixels with the same forest type that did not experience any burning and had a cumulative forest cover loss of <20% for the period from the year of fire occurrence up to the analysis year.
Recent trends in fire size and burnt area
Historical data for forest burnt areas and the number of fires for Canada, the USA and Australia were collated from a variety of sources (Supplementary Table 1).
For Canada, the fire event dataset consisted of point data retrieved from the Canadian National Fire Database (NFDB). This dataset includes the location and size of each individual fire event for 1960â2020. The NFDB, maintained by Natural Resources Canada, is derived from various Canadian fire management agencies including provinces, territories and Parks Canada. This dataset has been widely used in the analysis of long-term fire regime changes in Canada4,75.
For the USA, the burnt perimeter dataset for 1984â2020 from the MTBS project was used. The MTBS project mapped the fire extent and size of all large fires (that is, greater than 1,000âacres or 4.05âkm2 in the west and greater than 500âacres or 2.02âkm2 in the east) over the conterminous USA, Alaska and Hawaii76. This dataset has been previously used to analyse historical trends of large fires in the USA5.
We included Australia in our analysis, despite its location in the Southern Hemisphere, because its forests are prone to fire and can be largely classified as temperate. For Australia, polygon datasets of wildfire events (excluding prescribed fires) for 1981â2020 were obtained from the government agencies of land management and fire suppression for New South Wales, Western Australia, South Australia, Victoria, Queensland and Tasmania (Supplementary Table 1). These datasets have been extensively used in studies addressing the response of fire regimes to climate change in Australia77,78. The vegetation type for each fire polygon was determined based on the location of its centroid and its associated EAS CCI land cover type for 2001 to ensure that only forest fires were included.
Although the Canadian fire event data (NFDB) contain very detailed fire records including small fires (<2âkm2), in some agencies, the reporting of such fires only started at around 1980 (ref. 4). Moreover, previous studies have shown that small fires, although numerous, make up only a small fraction of the total area burnt79. To ensure consistency, only forest fires larger than 2âkm2 for Canada, USA and Australia were included in our analysis of temporal trends for fire size and burnt area.
Temporal trends in annual mean fire size, extreme fire size (95th percentile) and burnt area (Canada, 1960â2020; USA, 1984â2020; Australia, 1981â2020) were calculated using the MannâKendall test for trend and the TheilâSen slope estimator (Extended Data Fig. 10), both of which are robust to potential observation outliers1. The predicted values for the start and end years were obtained from the fitted TheilâSen regression. The relative change (%) in mean fire size and extreme fire size was calculated as the difference in the predicted value between the end and start years divided by the predicted value for the start year.
Further details are available in the Supplementary Information and refs. 80,81,82,83,84,85,86.