UK Biobank data processing and quality control
To conduct the rare variant burden analyses described in this study, we obtained WES data for 454,787 individuals from the UK Biobank study67. Participants were excluded on the basis of excess heterozygosity, autosomal variant missingness on genotyping arrays (â¥5%), or inclusion in the subset of phased samples as defined in Bycroft et al.68. Analysis was restricted to participants with European genetic ancestry, owing to the unknown influence of rare variants on population stratification and limited non-European sample size, leaving a total of 421,065 individuals. Variant quality control and annotation were performed using the UK Biobank Research Analysis Platform (RAP; https://ukbiobank.dnanexus.com/), a cloud-based central data repository for UK Biobank WES and phenotypic data. Besides the quality control described by Backman et al.67, we performed additional steps using custom applets designed for the RAP. First, we processed population-level variant call format (VCF) files by splitting and left-correcting multi-allelic variants into separate alleles using âbcftools normâ69. Second, we performed genotype-level filtering applying âbcftools filterâ separately for single nucleotide variants (SNVs) and insertionsâdeletion mutations using a missingness-based approach. Using this approach, we set to missing (./.) all SNV genotypes with depth <7 and genotype quality <20 or insertionâdeletion genotypes with a depth <10 and genotype quality <20. Next, we applied a binomial test to assess an expected alternate allele contribution of 50% for heterozygous SNVs; we set to missing all SNV genotypes with a binomial test P valueââ¤â1âÃâ10â3. Following genotype-level filtering we recalculated the proportion of individuals with a missing genotype for each variant and filtered all variants with a missingness valueâ>â50%. The variant annotation was performed using the ENSEMBL variant effect predictor (VEP) v10470 with the â–everythingâ flag and plugins for CADD71 and LOFTEE72 enabled. For each variant we prioritized the highest impact individual consequence as defined by VEP and one ENSEMBL transcript as determined by whether or not the annotated transcript was protein-coding, MANE select v0.97, or the VEP canonical transcript. Following annotation, variants were categorised on the basis of their predicted impact on the annotated transcript. PTVs were defined as all variants annotated as stop-gained, frameshift, splice acceptor and splice donor. Missense variant consequences are identical to those defined by VEP. Only autosomal or chromosome X variants within ENSEMBL protein-coding transcripts and within transcripts included on the UK Biobank ES assay67 were retained for subsequent burden testing.
Exome-wide association analyses in the UK Biobank
To perform rare variant burden tests, we used a custom implementation of BOLT-LMM v2.3.615 for the RAP. Two primary inputs are required by BOLT-LMM: (1) a set of genotypes with minor allele count >100 derived from genotyping arrays to construct a null linear mixed effects model; and (2) a larger set of variants collapsed on ENSEMBL transcript to perform association tests. For the former, we queried genotyping data available on the RAP and restricted to an identical set of individuals included for rare variant association tests. For the latter, and as BOLT-LMM expects imputed genotyping data as input rather than per-gene carrier status, we created dummy genotype files where each variant represents one gene and individuals with a qualifying variant within that gene are coded as heterozygous, regardless of the number of variants that individual has in that gene.
To test a range of variant annotation categories for MAFâ<â0.1%, we created dummy genotype files for high confidence PTVs as defined by LOFTEE, missense variants with CADDââ¥â25, and damaging variants that included both high confidence PTVs and missense variants with CADDââ¥â25. For each phenotype tested, BOLT-LMM was then run with default parameters other than the inclusion of the âlmmInfOnlyâ flag. To derive association statistics for individual markers, we also provided all 26,657,229 individual markers regardless of filtering status as input to BOLT-LMM. All tested phenotypes were run as continuous traits corrected by age, age2, sex, the first ten genetic principal components as calculated in Bycroft et al.68 and study participant ES batch as a categorical covariate (50k, 200k or 450k).
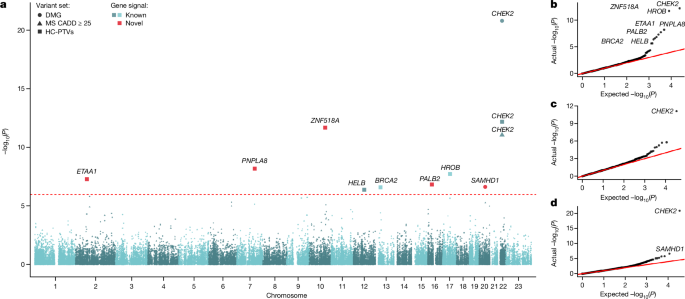
For discovery analysis in the primary trait of interest, ANM, we analysed 17,475 protein-coding genes with the minimum of 10 rare allele carriers in at least one of the masks tested using BOLT-LMM (Supplementary Table 1). The significant gene-level associations for ANM were identified applying Bonferroni correction for the number of masks with MACââ¥â10 (nâ=â46,251 masks) in 17,475 protein-coding genes (P: 0.05/46,251â=â1.08âÃâ10â6) (Supplementary Table 2). Furthermore, to compare and explain potential differences between our WES results and the previously published one5, we ran the above approach using MAFâ<â1%, a cut-off applied by Ward et al. (Supplementary Table 5 and Supplementary Information).
To generate accurate odds ratio and standard error estimates for binary traits, we also implemented a generalized linear model using the statsmodels package73 for Python in a three-step process. First, a null model was run with the phenotype as a continuous trait, corrected for control covariates as described above. Second, we regressed carrier status for individual genes on the residuals of the null model to obtain a preliminary P value. Thirdly, all genes were again tested using a full model to obtain odds ratios and standard errors with the family set to âbinomialâ. Generalized linear models utilized identical input to BOLT-LMM converted to a sparse matrix.
ANM phenotype derivation
ANM was derived for individuals within the UK Biobank, who were deemed to have undergone natural menopauseâthat is, not affected by surgical or pharmaceutical interventions, as follows.
First, European female participants (nâ=â245,820) who indicated during any of the attended visits having had a hysterectomy were collated (fields 3591 and 2724) and their reported hysterectomy ages were extracted (field 2824) and the median age was kept (nâ=â47,218 and 46,260 with reported ages). The same procedure was followed for participants indicating having undergone a bilateral oophorectomy (surgery field 2834 and age field 3882, nâ=â20,495 and 20,001 with reported ages).
For individuals having indicated the use of hormone-replacement therapy (HRT; field 2814), HRT start and end ages were collated (fields 3536 and 3546, accordingly) across the different attended visits (nâ=â98,104). In cases where the reported chronological HRT age at later attended visits was greater than that at previous visits, the later instances were prioritised, i.e. as they would potentially indicate an updated use of HRT. In cases where different HRT ages were reported, but not in chronologically increasing order, the median age was kept.
Menopausal status was determined using data across instances (field 2724) and prioritizing the latest reported data, to account for changes in menopause status. For participants indicating having undergone menopause, their reported ages at menopause were collated (field 3581) using the same procedure as for HRT ages (nâ=â158,264).
Exclusions were then applied to this age at menopause, as follows:
-
Participants reporting undergoing a hysterectomy and/or oophorectomy, but not the age at which this happened (nâ=â958 and 494, accordingly).
-
Participants reporting multiple hysterectomy and/or oophorectomy ages, which were more than 10 years apart (nâ=â38 and 23, accordingly).
-
Participants reporting multiple HRT start and/or end ages, which were not in chronologically ascending order and were more than 10 years apart (nâ=â124 and 137, accordingly).
-
Participants reporting multiple ages at menopause, which were not in chronologically ascending order and were more than 10 years apart (nâ=â73) and participants who reported both having and not having been through menopause and no other interventions (nâ=â98).
-
Participants having undergone a hysterectomy or oophorectomy before or during the year they report undergoing menopause.
-
Participants starting HRT prior to undergoing menopause and participants reporting HRT use, with no accompanying dates.
The resulting trait was representative of an ANM (nâ=â115,051) and was used in downstream analyses. Two additional ANM traits were also calculated, winsorized one by coding everyone reporting an ANM younger than 34, as 34 used in the discovery analysis as the primary phenotype (nâ=â115,051 total, reduced to 106,973 after covariate-resulting exclusions), and one by only including participants reporting ANM between 40 and 60, inclusive (nâ=â104,506), treated as a sensitivity analysis.
All manipulations were conducted in R (v4.1.2) on the UK Biobank RAP (https://ukbiobank.dnanexus.com/).
Replication of rare variant associations
Replication was performed using two study populations: the Icelandic deCODE study16,17 and the BRIDGES study18.
deCODE
The burden test associations are shown for three categories of rare variants with MAFâ<â2%; (1) loss-of-function (LOF) variants; (2) combination of LOF variants and predicted deleterious missense variants; and (3) combination of LOF variants and missense variants with CADD score ⥠25. We furthermore show results for category 3 using a more stringent frequency threshold, 0.1%. We included missense variants predicted to cause LOF by two meta-predictors, MetaSVM and MetaLR74, using variants available in dbNSFP v4.1c75. We used VEP70 to attribute predicted consequences to the variants sequenced. For caseâcontrol analyses, we used logistic regression and an additive model to test for association between LOF gene burdens and phenotypes, in which disease status was the dependent variable and genotype counts as the independent variable. Individuals were coded 1 if they carry any predicted LOF in the autosomal gene being tested and 0 otherwise. Age, sex and sequencing status of individuals was used as a covariate in the associations. For the analyses, we used software developed at deCODE genetics and we used linkage disequilibrium (LD) score regression intercepts76 to adjust the Ï2 statistics and avoid inflation due to cryptic relatedness and stratification. Quantitative traits were analysed using a linear mixed model implemented in BOLT-LMM15. To estimate the quality of the sequence variants across the entire set we regressed the alternative allele counts (AD) on the depth (DP) conditioned on the genotypes (GT) reported by GraphTyper77. For a well-behaving sequence variant, the mean alternative allele count for a homozygous reference genotype should be 0, for a heterozygous genotype it should be DP/2 and for homozygous alternative genotype it should be DP. Under the assumption of no sequencing or genotyping error, the expected value of AD should be DP conditioned on the genotype, in other words an identity line (slope 1 and intercept 0). Deviations from the identity line indicate that the sequence variant is spurious or somatic. We filter variants with slope less than 0.5. Additionally, GraphTyper employs a logistic regression model that assigns each variant a score (AAscore) predicting the probability that it is a true positive. We used only variants that have a AAscore > 0.8.
BRIDGES
The BRIDGES study included women from studies participating in the Breast Cancer Association Consortium (BCAC; v14) (http://bcac.ccge.medschl.cam.ac.uk/). The subset of population or hospital-based studies sampled independently of family history, together with population-matched controls (25 studies) were included in the analyses. ANM (years) was obtained from baseline questionnaire data. Women were considered as having experienced natural menopause if they indicated that the reason for menopause was reported as ânaturalâ or âunknownâ. Women were excluded from the analysis if the reason was indicated as either oophorectomy, hysterectomy, chemotherapy, stopping oral contraception or âany other reasonâ. Only studies with information on year of birth and age at menopause, and only women with reported age at menopause between ages twenty-five years and sixty years were included. All studies were approved by the relevant ethical review boards and used appropriate consent procedures.
Targeted sequencing of germline DNA from participants for 35 known or suspected breast cancer genes was performed, including the coding sequence and splice sites. Details of library preparation, sequencing, variant calling, and quality control procedures are described in Dorling et al.18. Carriers of PTVs in more than one of five main breast cancer susceptibility genes (BRCA1, BRCA2, ATM, CHEK2, PALB2) were excluded. Carriers of pathogenic missense variants (as defined by Dorling et al.18) in BRCA1 or BRCA2 were also excluded.
We carried out burden analyses, assessing the associations between rare variants in aggregate and ANM using linear regression, adjusting for country of origin, breast cancer case-control status and year of birth (categorized as up to 1935, 1936â1945, 1946â1955 or after 1956), and for some analyses body mass index (BMI). For each gene we considered PTVs in aggregate. The primary analyses included covariates to adjust for population, which was defined by country, with the exception of Malaysia and Singapore, in which the three distinct ethnic groups (Chinese, Indian and Malay) were treated as different strata and the UK, which was treated as separate strata (SEARCH, from East Anglia and PROCAS from north-west England). Sensitivity analyses were carried out adjusting for BMI in women with recorded age at BMI, and among women without a diagnosis of breast cancer. Sensitivity analyses were also carried out defining non-carriers as women not harbouring PTVs in the five main genes or pathogenic MSVs in BRCA1 and BRCA2.
WES sensitivity analysis using REGENIE
To replicate the primary findings and account for potential bias that could be introduced by exclusively using one discovery approach, a second analyst independently derived the age at menopause phenotype using a previously published method78 and conducted additional burden association analysis using the REGENIE regression algorithm (REGENIEv2.2.4; https://github.com/rgcgithub/regenie). REGENIE implements a generalized mixed-model region-based association test that can account for population stratification and sample relatedness in large-scale analyses. REGENIE runs in two steps79, which we implemented on the UK Biobank RAP. In the first step, genetic variants are aggregated into gene-specific units for each class of variant, called masks. We selected variants in CCDS transcripts deemed to be high confidence by LOFTEE72 with MAFâ<â0.1% and annotated using VEP70. We created three masks, independently of the primary analysis group: (1) LOF variants (stop-gain, frameshift, or abolishing a canonical splice site (â2 or +2âbp from exon, excluding the ones in the last exon)) or missense variants with CADD score >30; (2) LOF or missense variants with CADD score >25; and (3) all missense variants. In the second step, the three masks were tested for association with ANM. We applied an inverse normal rank transformation to ANM and included recruitment centre, sequence batch and 40 principal components as covariates. For each gene, we present results for the transcript with the smallest burden P value. We performed a sensitivity analysis, excluding women who had any cancer diagnosis before ANM (ICD10 C00-C97 excluding C44, ICD9 140-208 excluding 173; nâ=â2,585). The results for the sensitivity analyses performed via REGENIE are available in Supplementary Tables 1 and 2.
Common variant GWAS lookups
Genes within 500âkb upstream and downstream of the 290 lead SNPs from the latest GWAS of ANM1 were extracted from the exome-wide analysis. There were a total of 2149 genes within the GWAS regions. Burden tests in these genes with a Bonferroni corrected P value of <2.3âÃâ10â5 (0.05/2,149) were highlighted. The results are available in Supplementary Table 6.
Phenome-wide association analysis
To test the association of ANM identified genes in other phenotypes, we processed additional reproductive ageing-related phenotypes, including age at menarche, cancer, telomere length and sex hormones. All tested phenotypes were run as either continuous (age at menarche, telomere length and sex hormones) or binary traits (cancer) corrected by age, age2, sex, the first ten genetic principal components as calculated in Bycroft et al.68, and study participant ES batch as a categorical covariate (either 50k, 200k or 450k). Phenotype definitions and processing used in this study are described in Supplementary Tables 8 and 9. Only the first instance (initial visit) was used for generating all phenotype definitions unless specifically noted in Supplementary Table 8. In case of cancer-specific analysis, data from cancer registries, death records, hospital admissions and self-reported were harmonized to ICD10 coding. If a participant had a code for any of the cancers recorded in ICD10 (C00-C97) then they were counted as a case for this phenotype. Minimal filtering was performed on the data, with only those cases where a diagnosis of sex-specific cancer was given in contrast to the sex data contained in UK Biobank record 31, was a diagnosis not used. For more information on cancer-specific analysis refer to Supplementary Tables 9 and 11.
Cancer PheWAS associations
To test for an association between genes we identified as associated with menopause timing (Fig. 2 and Supplementary Table 2) and 90 individual cancers as included in cancer registries, death records, hospital admissions and self-reported data provided by UK Biobank (for example, breast, prostate, etc.) we utilised a logistic model with identical covariates as used during gene burden testing (nâ=â2430 tests) (Supplementary Tables 9 and 11). As standard logistic regression can lead to inflated test statistic estimates in cases of severe case/control imbalance80, we also performed a logistic regression with penalised likelihood estimation as described by Firth26 (Supplementary Table 11). Models were run as discussed in Kosmidis et al.81 using the brglm2 package implemented in R. brglm2 was run via the glm function with default parameters other than âfamilyâ set to âbinomialâ, method set to âbrglmFitâ, and type set to âAS_meanâ.
Expression in human female germ cells
We studied the mRNA abundance of WES genes during various stages of human female germ cell development using single-cell RNA sequencing data. We used the processed single cell RNA resequencing datasets from two published studies (Extended Data Figs. 6 and 7 and Supplementary Tables 17 and 18). This included single-cell RNA sequencing data from fetal primordial germ cells of human female embryos (accession code: GSE8614682), and from oocyte and granulosa cell fractions during various stages of follicle development (accession code: GSE10774683). A pseudo score of 1 was added to all values before log transformation of the dataset. The samples from fetal germ cells were categorized into sub-clusters as defined in the original study. The study by Li et al.82 identified 17 clusters by performing a t-distributed stochastic neighbour embedding analysis and using expression profiles of known marker genes for various stages of fetal germ cell development. In our analysis we have included four clusters of female fetal germ cells (mitotic, retinoic acid-responsive, meiotic and oogenesis) and four clusters containing somatic cells in the fetal gonads (endothelial, early_granulosa, mural_granulosa and late_granulosa). Software packages for Râtidyverse (https://www.tidyverse.org/), pheatmap, (https://CRAN.R-project.org/package=pheatmap) and reshape2 (https://github.com/hadley/reshape)âwere used in processing and visualising the data.
De novo mutation rate analyses in 100kGP
Constructing PGSs
We calculated PGSs in participants from the rare disease programme of the 100kGP v14. There are 77,901 individuals in the aggregated variant calls (aggV2) after excluding participants whose genetically inferred sex is not consistent with their phenotypic sex. We restricted the PGS analysis to individuals of European ancestry, which was predicted by the Genomics England bioinformatics team using a random forest model based on genetic principal components generated by projecting aggV2 data onto the 1000 Genomes phase 3 principal component loadings. We removed one sample in each pair of related probands with kinship coefficient > 1/(24.5)âthat is, up to and including third-degree relationships. Probands with the highest number of relatives were removed first. Similarly, we retained unrelated mothers and fathers of these unrelated probands. It left us with 8,089 motherâoffspring duos and 8,029 fatherâoffspring duos.
We used the lead variants (or proxies, as described below) for genome-wide significant loci previously reported for ANM1 to calculate PGS in the parents. In 100kGP, we removed variants with MAFâ<â0.5% or missing rate >5% from the aggV2 variants prepared by the Genomics England bioinformatics team. For lead variants that did not exist in 100kGP, we used the most significant proxy variants with LD r2â>â0.5 if available in 100kGP. This resulted in a PGS constructed from 287 of the 290 previously reported loci. We regressed out 20 genetic principal components that were calculated within the European subset from the PGS and scaled the residuals to have meanâ=â0 and s.d.â=â1. Higher PGS indicates later ANM.
Calling de novo mutations
De novo mutations (DNMs) were called using the Platypus variant caller in 10,478 parent offspring trios by the Genomics England Bioinformatics team. The detailed analysis pipeline is documented at: https://research-help.genomicsengland.co.uk/display/GERE/De+novo+variant+research+dataset. Extensive quality control and filtering were applied as described previously31. In brief, multiple filters were applied, including the following:
-
the child had a heterozygous genotype and parents were homozygous reference.
-
the parents had <2 reads supporting the alternate allele.
-
read depth >20 in child and parents.
-
variant allele fraction (VAF)â>0.3 and <0.7 in the child.
-
no DNMs were clustered (within 20âbp).
Autosomal de novo SNVs (dnSNVs) were phased using reads or read pairs that contained both the dnSNV and heterozygous variants located within 500âbp of it. A DNM was phased to a parent when the DNM appeared exclusively on the same haplotype as its nearby heterozygous variant. About one third of the dnSNVs were phased, of which three quarters were paternally phased (Extended Data Fig. 5 and Supplementary Table 14).
Associating the ANM PGS with DNMs in 100kGP
In association models, we accounted for parental age, the primary determinant of the number of DNMs, and various data quality metrics as described31:
-
Mean coverage for the child, mother and father (child_mean_RD, mother_mean_RD, father_mean_RD).
-
Proportion of aligned reads for the child, mother and father (child_prop_aligned, mother_prop_aligned, father_prop_aligned).
-
Number of SNVs called for child, mother and father (child_SNVs, mother_SNVs, father_SNVs).
-
Median variant allele fraction of DNMs called in child (median_VAF).
-
Median Bayes factor as output by Platypus for DNMs called in the child. This is a metric of DNM quality (median_BF).
We first tested the association between parental PGSs and total de novo autosomal SNV count in the offspring in a Poisson regression with an identity link:
$$\begin{array}{l}{\rm{dnSNVs}}\_{\rm{total}}={\beta }_{0}+{\beta }_{1}\mathrm{PGS}({\rm{paternal\; or\; maternal}})\\ \,\,+{\beta }_{2}{\rm{paternal}}\_{\rm{a}}{\rm{g}}{\rm{e}}+{\beta }_{3}{\rm{maternal}}\_{\rm{a}}{\rm{g}}{\rm{e}}{+\beta }_{4}{\rm{child}}\_{\rm{m}}{\rm{e}}{\rm{a}}{\rm{n}}\_{\rm{R}}{\rm{D}}\\ \,\,+{\beta }_{5}{\rm{m}}{\rm{o}}{\rm{t}}{\rm{h}}{\rm{e}}{\rm{r}}\_{\rm{m}}{\rm{e}}{\rm{a}}{\rm{n}}\_{\rm{R}}{\rm{D}}+{\beta }_{6}{\rm{f}}{\rm{a}}{\rm{t}}{\rm{h}}{\rm{e}}{\rm{r}}\_{\rm{m}}{\rm{e}}{\rm{a}}{\rm{n}}\_{\rm{R}}{\rm{D}}\\ \,\,+\,{\beta }_{7}{\rm{c}}{\rm{h}}{\rm{i}}{\rm{l}}{\rm{d}}{\rm{\_}}{\rm{p}}{\rm{r}}{\rm{o}}{\rm{p}}{\rm{\_}}{\rm{a}}{\rm{l}}{\rm{i}}{\rm{g}}{\rm{n}}{\rm{e}}{\rm{d}}+{\beta }_{8}{\rm{m}}{\rm{o}}{\rm{t}}{\rm{h}}{\rm{e}}{\rm{r}}{\rm{\_}}{\rm{p}}{\rm{r}}{\rm{o}}{\rm{p}}{\rm{\_}}{\rm{a}}{\rm{l}}{\rm{i}}{\rm{g}}{\rm{n}}{\rm{e}}\\ \,\,+{\beta }_{9}{\rm{f}}{\rm{a}}{\rm{t}}{\rm{h}}{\rm{e}}{\rm{r}}{\rm{\_}}{\rm{p}}{\rm{r}}{\rm{o}}{\rm{p}}{\rm{\_}}{\rm{a}}{\rm{l}}{\rm{i}}{\rm{g}}{\rm{n}}{\rm{e}}{\rm{d}}+{\beta }_{10}{\rm{c}}{\rm{h}}{\rm{i}}{\rm{l}}{\rm{d}}{\rm{\_}}{\rm{s}}{\rm{n}}{\rm{v}}{\rm{s}}\\ \,\,+{\beta }_{11}{\rm{m}}{\rm{o}}{\rm{t}}{\rm{h}}{\rm{e}}{\rm{r}}{\rm{\_}}{\rm{s}}{\rm{n}}{\rm{v}}{\rm{s}}+{\beta }_{12}{\rm{f}}{\rm{a}}{\rm{t}}{\rm{h}}{\rm{e}}{\rm{r}}{\rm{\_}}{\rm{s}}{\rm{n}}{\rm{v}}{\rm{s}}\\ \,\,+{\beta }_{13}{\rm{m}}{\rm{e}}{\rm{d}}{\rm{i}}{\rm{a}}{\rm{m}}{\rm{\_}}{\rm{V}}{\rm{A}}{\rm{F}}+{\beta }_{14}{\rm{m}}{\rm{e}}{\rm{d}}{\rm{i}}{\rm{a}}{\rm{n}}{\rm{\_}}{\rm{B}}{\rm{F}}\end{array}$$
We also fitted Poisson regression models to test the association between the PGS of one of the parents and the dnSNVs in the offspring that were phased to the relevant parent. We supplied 0.5 as the starting value for all coefficients when running the glm() function in R with an identity link. Using a different starting value (for example, 0.2 and 10) did not change the coefficient estimates.
The paternal model included paternal PGS, age and data quality metrics that are related to the proband and the father:
$$\begin{array}{l}{\rm{dnSNVs}}\_{\rm{paternal}}={\beta }_{0}+{\beta }_{1}{\rm{paternal}}\_{\rm{P}}{\rm{G}}{\rm{S}}+{\beta }_{2}{\rm{paternal}}\_{\rm{a}}{\rm{g}}{\rm{e}}\\ \,\,\,+\,{\beta }_{3}{\rm{c}}{\rm{h}}{\rm{i}}{\rm{l}}{\rm{d}}\_{\rm{m}}{\rm{e}}{\rm{a}}{\rm{n}}\_{\rm{R}}{\rm{D}}+{\beta }_{4}{\rm{f}}{\rm{a}}{\rm{t}}{\rm{h}}{\rm{e}}{\rm{r}}\_{\rm{m}}{\rm{e}}{\rm{a}}{\rm{n}}\_{\rm{R}}{\rm{D}}\\ \,\,\,+\,{\beta }_{5}{\rm{c}}{\rm{h}}{\rm{i}}{\rm{l}}{\rm{d}}\_{\rm{p}}{\rm{r}}{\rm{o}}{\rm{p}}\_{\rm{aligned}}+{\beta }_{6}{\rm{f}}{\rm{a}}{\rm{t}}{\rm{h}}{\rm{e}}{\rm{r}}\_{\rm{p}}{\rm{r}}{\rm{o}}{\rm{p}}\_{\rm{aligned}}\\ \,\,\,+\,{\beta }_{7}{\rm{c}}{\rm{h}}{\rm{i}}{\rm{l}}{\rm{d}}\_{\rm{s}}{\rm{n}}{\rm{v}}{\rm{s}}+{\beta }_{8}{\rm{f}}{\rm{a}}{\rm{t}}{\rm{h}}{\rm{e}}{\rm{r}}\_{\rm{s}}{\rm{n}}{\rm{v}}{\rm{s}}\\ \,\,\,+\,{\beta }_{9}{\rm{median}}\_{\rm{V}}{\rm{A}}{\rm{F}}+{\beta }_{10}{\rm{median}}\_{\rm{B}}{\rm{F}}\end{array}$$
Similarly, the maternal model was as follows:
$$\begin{array}{l}{\rm{dnSNVs}}\_{\rm{m}}{\rm{a}}{\rm{t}}{\rm{e}}{\rm{r}}{\rm{n}}{\rm{a}}{\rm{l}}={\beta }_{0}+{\beta }_{1}{\rm{m}}{\rm{a}}{\rm{t}}{\rm{e}}{\rm{r}}{\rm{n}}{\rm{a}}{\rm{l}}\_{\rm{P}}{\rm{G}}{\rm{S}}+{\beta }_{2}{\rm{m}}{\rm{a}}{\rm{t}}{\rm{e}}{\rm{r}}{\rm{n}}{\rm{a}}{\rm{l}}\_{\rm{a}}{\rm{g}}{\rm{e}}\\ \,\,\,+\,{\beta }_{3}{\rm{c}}{\rm{h}}{\rm{i}}{\rm{l}}{\rm{d}}\_{\rm{m}}{\rm{e}}{\rm{a}}{\rm{n}}\_{\rm{R}}{\rm{D}}+{\beta }_{4}{\rm{mother}}\_{\rm{m}}{\rm{e}}{\rm{a}}{\rm{n}}\_{\rm{R}}{\rm{D}}\\ \,\,\,+\,{\beta }_{5}{\rm{c}}{\rm{h}}{\rm{i}}{\rm{l}}{\rm{d}}\_{\rm{p}}{\rm{r}}{\rm{o}}{\rm{p}}\_{\rm{aligned}}+{\beta }_{6}{\rm{mother}}\_{\rm{p}}{\rm{r}}{\rm{o}}{\rm{p}}\_{\rm{aligned}}\\ \,\,\,+\,{\beta }_{7}{\rm{c}}{\rm{h}}{\rm{i}}{\rm{l}}{\rm{d}}\_{\rm{s}}{\rm{n}}{\rm{v}}{\rm{s}}+{\beta }_{8}{\rm{mother}}\_{\rm{s}}{\rm{n}}{\rm{v}}{\rm{s}}\\ \,\,\,+\,{\beta }_{9}{\rm{median}}\_{\rm{V}}{\rm{A}}{\rm{F}}+{\beta }_{10}{\rm{median}}\_{\rm{B}}{\rm{F}}\end{array}$$
Finally, as a check, we assessed the association between the maternal PGS and paternally phased dnSNVs, and vice versa, using a Poisson regression with an identity link where the same starting value for coefficients were supplied:
$$\begin{array}{l}{\rm{dnSNVs}}\_{\rm{p}}{\rm{a}}{\rm{t}}{\rm{e}}{\rm{r}}{\rm{n}}{\rm{a}}{\rm{l}}={\beta }_{0}+{\beta }_{1}{\rm{m}}{\rm{a}}{\rm{t}}{\rm{e}}{\rm{r}}{\rm{n}}{\rm{a}}{\rm{l}}\_{\rm{P}}{\rm{G}}{\rm{S}}+{\beta }_{2}{\rm{p}}{\rm{a}}{\rm{t}}{\rm{e}}{\rm{r}}{\rm{n}}{\rm{a}}{\rm{l}}\_{\rm{a}}{\rm{g}}{\rm{e}}\\ \,\,\,+\,{\beta }_{3}{\rm{c}}{\rm{h}}{\rm{i}}{\rm{l}}{\rm{d}}\_{\rm{m}}{\rm{e}}{\rm{a}}{\rm{n}}\_{\rm{R}}{\rm{D}}+{\beta }_{4}{\rm{f}}{\rm{a}}{\rm{t}}{\rm{h}}{\rm{e}}{\rm{r}}\_{\rm{m}}{\rm{e}}{\rm{a}}{\rm{n}}\_{\rm{R}}{\rm{D}}\\ \,\,\,+\,{\beta }_{5}{\rm{c}}{\rm{h}}{\rm{i}}{\rm{l}}{\rm{d}}\_{\rm{p}}{\rm{r}}{\rm{o}}{\rm{p}}\_{\rm{a}}{\rm{l}}{\rm{i}}{\rm{g}}{\rm{n}}{\rm{e}}{\rm{d}}+{\beta }_{6}{\rm{f}}{\rm{a}}{\rm{t}}{\rm{h}}{\rm{e}}{\rm{r}}\_{\rm{p}}{\rm{r}}{\rm{o}}{\rm{p}}\_{\rm{a}}{\rm{l}}{\rm{i}}{\rm{g}}{\rm{n}}{\rm{e}}{\rm{d}}\\ \,\,\,+\,{\beta }_{7}{\rm{c}}{\rm{h}}{\rm{i}}{\rm{l}}{\rm{d}}\_{\rm{s}}{\rm{n}}{\rm{v}}{\rm{s}}+{\beta }_{8}{\rm{f}}{\rm{a}}{\rm{t}}{\rm{h}}{\rm{e}}{\rm{r}}\_{\rm{s}}{\rm{n}}{\rm{v}}{\rm{s}}\\ \,\,\,+\,{\beta }_{9}{\rm{m}}{\rm{e}}{\rm{d}}{\rm{i}}{\rm{a}}{\rm{n}}\_{\rm{V}}{\rm{A}}{\rm{F}}+{\beta }_{10}{\rm{m}}{\rm{e}}{\rm{d}}{\rm{i}}{\rm{a}}{\rm{n}}\_{\rm{B}}{\rm{F}}\end{array}$$
$$\begin{array}{l}{\rm{dnSNVs}}\_{\rm{maternal}}={\beta }_{0}+{\beta }_{1}{\rm{paternal}}\_{\rm{P}}{\rm{G}}{\rm{S}}+{\beta }_{2}{\rm{maternal}}\_{\rm{a}}{\rm{g}}{\rm{e}}\\ \,\,\,+\,{\beta }_{3}{\rm{c}}{\rm{h}}{\rm{i}}{\rm{l}}{\rm{d}}\_{\rm{m}}{\rm{e}}{\rm{a}}{\rm{n}}\_{\rm{R}}{\rm{D}}+{\beta }_{4}{\rm{mother}}\_{\rm{m}}{\rm{e}}{\rm{a}}{\rm{n}}\_{\rm{R}}{\rm{D}}\\ \,\,\,+\,{\beta }_{5}{\rm{c}}{\rm{h}}{\rm{i}}{\rm{l}}{\rm{d}}\_{\rm{p}}{\rm{r}}{\rm{o}}{\rm{p}}\_{\rm{aligned}}+{\beta }_{6}{\rm{mother}}\_{\rm{p}}{\rm{r}}{\rm{o}}{\rm{p}}\_{\rm{aligned}}\\ \,\,\,+\,{\beta }_{7}{\rm{c}}{\rm{h}}{\rm{i}}{\rm{l}}{\rm{d}}\_{\rm{s}}{\rm{n}}{\rm{v}}{\rm{s}}+{\beta }_{8}{\rm{mother}}\_{\rm{s}}{\rm{n}}{\rm{v}}{\rm{s}}\\ \,\,\,+\,{\beta }_{9}{\rm{median}}\_{\rm{V}}{\rm{A}}{\rm{F}}+{\beta }_{10}{\rm{median}}\_{\rm{B}}{\rm{F}}\end{array}$$
Rare variant burden in ANM genes in 100kGP
We tested for association between the burden of rare coding variants in ANM-associated genes in mothers and fathers with phased de novo SNVs in their offspring. We extracted high-confidence PTVs annotated by LOFTEE in the nine genes associated with ANM at the exome-wide significance (Fig. 2), as well as damaging missense variants with CADDâ>â25 in CHEK2 and SAMHD1. Annotations were extracted from VEP105. All variants had MAFâ<â0.1% in the 100kGP aggV2 dataset and in all sub-populations in gnomAD. We set to missing genotypes with depth <7 and genotype quality <20 or heterozygous genotypes with a binomial test Pâ<â0.001.
We first regressed out the same covariates as described above in the PGS analysis from maternally phased DNMs using a linear regression. We applied a rank-based inverse normal transformation on the residuals and fitted a linear regression model of the adjusted DNMs on carrier status in unrelated mothers for each of the 9 genes that were associated with ANM, adjusting for 20 genetic principal components. We adjusted paternally phased DNMs and regressed it on gene burden similarly in unrelated fathers.
Mendelian randomization
Instrumental variable selection
Mendelian randomization analysis was applied to test whether the common variants associated with ANM1 have a causal effect on DNM rates in the offspring (Supplementary Table 15). In this approach, genetic variants that are significantly associated with an exposure, in this case ANM, are used as instrumental variables to test the causality of that exposure on the outcome of interest, in this case DNM rate84,85,86. For a genetic variant to be a reliable instrument, the following assumptions should be met: (1) the genetic instrument is associated with the exposure of interest; (2) the genetic instrument should not be associated with any other competing risk factor that is a confounder; and (3) the genetic instrument should not be associated with the outcome, except via the causal pathway that includes the exposure of interest84,87. Genotypes at all variants were aligned to designate the ANM PGS-increasing alleles as the effect alleles as described above and this was used as a genetic instrument of interest. The effect sizes of genetic instruments (genotypes in the mother) on maternally phased de novo SNVs in the offspring estimated in 8,089 duos were obtained from Genomics England.
Mendelian randomization frameworks
The Mendelian randomization analysis was conducted using the inverse-variance weighted (IVW) model as the primary model due to the highest statistical power88. However, as it does not correct for heterogeneity in outcome risk estimates between individual variants89, we applied a number of sensitivity Mendelian randomization methods that better account for heterogeneity90. These include Mendelian randomization Egger to identify and correct for unbalanced heterogeneity (âhorizontal pleiotropyâ), indicated by a significant Egger intercept (Pâ<â0.05)91, and weighted median (WM) and penalized weighted median (PWM) models to correct for balanced heterogeneity92. In addition, we introduced the Mendelian randomization radial method to exclude variants from each model in cases where they are recognized as outliers93. The results were considered as significant based on the P value significance consistency across different primary and sensitivity models applied. The results are available in Supplementary Table 15.
Analyses of DNMs in deCODE
Identifying DNMs
The genome of the Icelandic population was characterised by whole-genome sequencing of 63,460 Icelanders using Illumina standard TruSeq methodology to a mean depth of 35 Ã (s.d. 8Ã) with subsequent long-range phasing16. Analyses of DNMs were restricted to individuals with at least 20Ã coverage.
DNM candidates were called in 9,643 trios in a similar manner to that described previously32,33, by comparing the genotypes of the parents and offspring. In brief, we defined a DNM candidate with permissive cut-offs for the genotype of the proband requiring that allele balance is greater than 25% and that there be at least 12 reads at the position (supporting either the reference or alternative allele). For the genotypes of the parents, we required at least 12 reads, maximum of one read supporting the alternative allele and the allelic balance to be less than 5%. Likely (NLIK) and possible carriers (NPOSS) of the DNM allele outside the descendants of the parent pair were defined as before32. We restricted to DNM candidates with fewer than 50 likely carriers and either fewer than 10 possible carriers or with a ratio NLIK/NPOSS greater than 80%.
We tuned the DNM candidate filtering by using segregation of DNM candidates in three-generation families (2,042 probands), following32. We restricted to instances of the DNM candidates where we see both of the probandâs haplotypes at a locus transmitted to the offspring of the proband (see fig. 1c in ref. 32). In brief, if the DNM is a true germline variant then the allele of the DNM candidate should be present in the offspring who inherited the haplotype on which it lies. On the other hand, if it is absent from the children, despite both the haplotypes of the proband having been transmitted to at least one offspring, this suggests that the DNM candidate is a false-positive DNM call (see more detailed description in ref. 32). As before32, we fitted the generalized additive model with a logistic link using the mgcv R package94, using various functions of the following quality metrics as covariates, as indicated in the code:
-
AAScore: prediction probability from Graphtyper that the variant is a true positive.
-
Carrier_regression_beta: slope from the alternative allele depth regression for the sequence variant (described in the burden method section from deCODE).
-
Carrier_regression_alpha: intercept from the alternative allele depth regression for the sequence variant (described in the burden method section from deCODE).
-
Proband_het_AB: the allelic balance of the proband.
-
MaxAAS: the maximum read support for the sequence variant across all individuals.
-
Alignment_Alt_Reads: the number of reads supporting the alternative allele. This covariate and the following covariates were derived by identifying the reads in the BAM files supporting the de novo allele.
-
Alignment_Alt_Unique_Positions: the unique number of starting positions for the reads supporting the alternative allele.
-
Alignment_Alt_Soft_clipped: the number of soft clipped bases (S in CIGAR string).
-
Alignment_Alt_Matched_bases: the number of matched bases (M in CIGAR string).
-
Alignment_Alt_Score_diff: the difference in the alignment score between the best and the second best hit as reported by BWA mem.
-
Alignment_Alt_Pair_sw_nm: the pairwise mismatches between reads supporting the alternative allele using the Smith Waterman implementation in SeqAn95.
-
Alignment_Alt_Pair_align: the number of bases in the pairwise alignments.
We fitted the following formula within the gam() function in the mgcv R package94:
threegen_Consistent_hs~
I(cut(alignment_Alt_Unique_Positions,c(â1,2,4,8,10,Inf)))+
s(I(AAScore))+
s(Carrier_regression_beta)+
s(Carrier_regression_alpha)+
I(ifelse(alignment_Alt_Reads>0,
(alignment_Alt_Score_diff/alignment_Alt_Reads)>10,
FALSE))+
I(ifelse(alignment_Alt_Pair_align>0,
(alignment_Alt_Pair_sw_nm/alignment_Alt_Pair_align)>0.05,
TRUE))+
I(ifelse(alignment_Alt_Matched_bases>0,
alignment_Alt_Soft_clipped/alignment_Alt_Matched_bases>0.5,
TRUE))+
s(Proband_het_AB)+
s(ifelse(MaxAAS>15,
16,
MaxAAS))+
I(NPOSSâ=â=â0)
We then took the model learned using informative DNMs in these three-generation families and applied it to all remaining DNM candidates. We retained candidate DNMs for which the predicted probability of being a real DNM based on this model was at least 50%.
To validate the false-positive detection rate of the DNMs, we also used the genotype consistency between pairs of monozygotic twins. We found that 3.8% of DNMs are unobserved in the monozygotic twin of the proband. These could either be false-positive DNM calls or high frequency post-zygotic mutations that differ between pairs of monozygotic twins96.
To mirror the analysis of 100kGP, we phased the DNMs using read-backed phasing as previously described32.
Associating the ANM PGS with DNMs in deCODE
We calculated the raw ANM PGS per individual by multiplying the effect estimate by the count of the effect allele and summing the product across SNPs. We rank-transformed the raw PGS distribution across individuals to a standardized normal distribution. We fitted the following Poisson regression with identity link to assess the association between the motherâs PGS and the number of maternally phased DNMs:
$$\begin{array}{l}{\rm{dnSNVs}}\_{\rm{m}}{\rm{a}}{\rm{t}}{\rm{e}}{\rm{r}}{\rm{n}}{\rm{a}}{\rm{l}} \sim {\rm{maternal}}\_{\rm{P}}{\rm{G}}{\rm{S}}+{\rm{m}}{\rm{a}}{\rm{t}}{\rm{e}}{\rm{r}}{\rm{n}}{\rm{a}}{\rm{l}}\_{\rm{a}}{\rm{g}}{\rm{e}}\\ \,\,\,+\,{\rm{p}}{\rm{a}}{\rm{t}}{\rm{e}}{\rm{r}}{\rm{n}}{\rm{a}}{\rm{l}}\_{\rm{c}}{\rm{o}}{\rm{v}}{\rm{e}}{\rm{r}}{\rm{a}}{\rm{g}}{\rm{e}}\,+\,{\rm{maternal}}\_{\rm{c}}{\rm{o}}{\rm{v}}{\rm{e}}{\rm{r}}{\rm{a}}{\rm{g}}{\rm{e}}\\ \,\,\,+\,{\rm{c}}{\rm{h}}{\rm{i}}{\rm{l}}{\rm{d}}\_{\rm{c}}{\rm{o}}{\rm{v}}{\rm{e}}{\rm{r}}{\rm{a}}{\rm{g}}{\rm{e}}\,+\,{\rm{G}}{\rm{A}}{\rm{M}}\_{\rm{P}}{\rm{r}}{\rm{e}}{\rm{d}}{\rm{i}}{\rm{c}}{\rm{t}}\_{\rm{M}}{\rm{e}}{\rm{a}}{\rm{n}}\end{array}$$
where GAM_Predict_Mean is the average probability of the DNMs in the probands being real, calculated using the method described above.
We also fitted the following models as negative controls:
$$\begin{array}{l}{\rm{dnSNVs}}\_{\rm{paternal}} \sim {\rm{paternal}}\_{\rm{P}}{\rm{G}}{\rm{S}}+{\rm{paternal}}\_{\rm{a}}{\rm{g}}{\rm{e}}\\ \,\,\,+\,{\rm{paternal}}\_{\rm{coverage}}+{\rm{maternal}}\_{\rm{coverage}}\\ \,\,\,+{\rm{c}}{\rm{h}}{\rm{i}}{\rm{l}}{\rm{d}}\_{\rm{coverage}}+{\rm{G}}{\rm{A}}{\rm{M}}\_{\rm{Predict}}\_{\rm{M}}{\rm{e}}{\rm{a}}{\rm{n}}\end{array}$$
$$\begin{array}{l}{\rm{dnSNVs}}\_{\rm{paternal}} \sim {\rm{maternal}}\_{\rm{P}}{\rm{G}}{\rm{S}}+{\rm{paternal}}\_{\rm{a}}{\rm{g}}{\rm{e}}\\ \,\,\,+\,{\rm{paternal}}\_{\rm{coverage}}+{\rm{materna}}\_{\rm{coverage}}\\ \,\,\,+{\rm{c}}{\rm{h}}{\rm{i}}{\rm{l}}{\rm{d}}\_{\rm{coverage}}+{\rm{G}}{\rm{A}}{\rm{M}}\_{\rm{P}}{\rm{r}}{\rm{e}}{\rm{d}}{\rm{i}}{\rm{c}}{\rm{t}}\_{\rm{M}}{\rm{e}}{\rm{a}}{\rm{n}}\end{array}$$
To fit these models, we randomly chose one offspring per family.
ANM genetic variants and DNMs in deCODE
We analysed variants with MAFâ<â2%. This was a higher threshold than had been used in 100kGP since our analyses of ANM associations indicated that this threshold appeared to be better powered within deCODE, possibly because some deleterious variants have risen to a higher frequency due to the Icelandic bottleneck. We focused on PTVs in the nine genes associated with ANM at the exome-wide significance (Fig. 2), as well as damaging missense variants with CADDâ>â25 in CHEK2 and SAMHD1.
For maternally and paternally phased DNMs, we adjusted the number of DNM for parental ages at conception and normalized the trait using rank-based inverse normal transformation. A linear regression model was used to test for association between the transformed DNM rate and the burden genotypes, assuming the variance-covariance matrix to be proportional to the kinship matrix.
We used an inverse-variance weighted approach to meta-analyse the results from 100kGP and deCODE. A Bonferroni correction of 18 tests (9 genes and 2 parents) was applied.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.