Signatures of magnetism control by flow of angular momentum

Sample preparation

Samples with various Fe thicknesses t_Fe are grown by molecular-beam epitaxy (MBE). First, a GaAs buffer layer of 100 nm is grown in a III–V MBE. After that the substrate (semi-insulating wafer, which has a resistivity ρ between 1.72 × 10⁸ Ω cm and 2.16 × 10⁸ Ω cm) is transferred to a metal MBE without breaking the vacuum for the growth of the metal layers. For a better comparison of the physical properties of different samples, various Fe thicknesses are grown on a single two-inch wafer by stepping the main shadow shutter of the metal MBE. After the growth of the step-wedged Fe film, 1.5-nm Al/6-nm Pt layers are deposited on the whole wafer. Sharp reflection high-energy electron diffraction patterns have been observed after the growth of each layer (Supplementary Note 1), which indicate the epitaxial growth mode as well as good surface (interface) flatness. High-resolution transmission electron microscopy measurements (Supplementary Note 1) show that (1) all the layers are crystalline and (2) there is diffusion of Al into Pt but no significant Al–Fe and Pt–Fe interdiffusion. Therefore, the magnetic proximity effect between Fe and Pt is reduced. The intermixed Pt–Al alloy can be a good spin current generator. Previous work⁴⁹ has shown that alloying Pt with Al enhances the spin-torque efficiency.

Device fabrication

First, Pt/Al/Fe stripes with a dimension of 4 μm × 20 μm and with the long side along the [110] and [100] orientations are defined by a mask-free writer and Ar-etching. After that, contact pads for the application of the d.c. current, which are made from 3-nm Ti and 50 nm Au, are prepared by evaporation and lift-off. Then, a 70-nm Al₂O₃ layer is deposited by atomic layer deposition to electrically isolate the d.c. contacts and the coplanar waveguide (CPW). Finally, the CPW consisting of 5 nm Ti and 150 nm Au is fabricated by evaporation, and the Fe/Al/Pt stripes are located in the gap between the signal line and ground line of the CPW (Fig. 2a). During the fabrication, the highest baking temperature is 110 °C. The CPW is designed to match the radiofrequency network that has an impedance of 50 Ω. The width of the signal line and the gap are 50 μm and 30 μm, respectively. Magnetization dynamics of Fe are excited by out-of-plane Oersted field induced by the radiofrequency microwave currents flowing in the signal and ground lines.

FMR measurements

The FMR method is used in this study for several reasons: (1) FMR has a higher sensitivity than static magnetization measurements. (2) The FMR method, together with angle and frequency-dependent measurements, is a standard way to quantify the effective magnetization, magnetic anisotropies and Gilbert damping. (3) Damping-like and field-like torques can be determined simultaneously in a single experiment, and thus we can establish a connection between damping-like torque and the modification of magnetic anisotropies. (4) The Joule heating effect, which also alters the magnetic properties of Fe, can be easily excluded from the I dependence of H_R.

The FMR spectra are measured optically by time-resolved magneto-optical Kerr microscopy; a pulse train of a Ti:sapphire laser (repetition rate of 80 MHz and pulse width of 150 fs) with a wavelength of 800 nm is phase-locked to a microwave current. A phase shifter is used to adjust the phase between the laser pulse train and microwave, and the phase is kept constant during the measurement. The polar Kerr signal at a certain phase, V_Kerr, is detected by a lock-in amplifier by phase modulating the microwave current at a frequency of 6.6 kHz. The V_Kerr signal is measured by sweeping the external magnetic field, and the magnetic field can be rotated in-plane by 360°. A Keithley 2400 device is used as the d.c. current source for linewidth and resonance field modifications. All measurements are performed at room temperature.

The FMR spectra are well fitted by combining a symmetric (L_sym = ΔH²/[4(H − H_R)²â€‰+ ΔH²]) and an anti-symmetric Lorentzian (L_a-sym = −4ΔH(H − H_R)/[4(H − H_R)²â€‰+ ΔH²]), V_Kerr = V_symL_sym + V_a-symL_a-sym + V_offset, where H_R is the resonance field, ΔH is the full width at half maximum, V_offset is the offset voltage, and V_sym (V_a-sym) is the magnitude of the symmetric (anti-symmetric) component of V_Kerr. It is worth mentioning that, by analysing the position of H_R, we have also confirmed that the application of the charge currents does not have a detrimental effect on the magnetic properties of the Fe films (Supplementary Note 2).

Magnetic anisotropies in Pt/Al/Fe/GaAs multilayers

A typical in-plane magnetic field angle φ_H dependence of the resonance field H_R for t_Fe = 1.2 nm measured at f = 13 GHz is shown in Extended Data Fig. 2a. The sample shows typical in-plane uniaxial anisotropy with two-fold symmetry, that is, a magnetically HA for φ_H = −45° and 135° (\(\langle \bar{1}10\rangle \) orientations) and a magnetically EA for φ_H = 45° and 225° (⟨110⟩ orientations), which originates from the anisotropic bonding at the Fe/GaAs interface³³. To quantify the magnitude of the anisotropies, we further measure the f dependence of H_R both along the EA and the HA (Extended Data Fig. 2b). Both the angle and frequency dependence of H_R are fitted according to^34,50

with \({H}_{1}^{\text{R}}\) = H^R cos(φ − φ_H) + H_K + H_B(3 + cos 4φ)/4 − H_U sin²(φ − 45°) and \({H}_{2}^{\text{R}}\) = H^R cos(φ − φ_H) +  H_B cos 4φ − H_U sin 2φ. Here γ (= gμ_B/ħ) is the gyromagnetic ratio, g is the Landé g-factor, μ_B is the Bohr magneton, ħ is the reduced Planck constant, H_K (= M − H_⊥) is the effective demagnetization magnetic anisotropy field, including the perpendicular magnetic anisotropy field H_⊥, H_B is the biaxial magnetic anisotropy field along the ⟨100⟩ orientations, H_U is the in-plane UMA field along ⟨110⟩ orientations and φ is the in-plane angle of magnetization as defined in Extended Data Fig. 1. The magnitude of φ is obtained by the equilibrium condition

It can be checked that φ = φ_H holds when H is along ⟨110⟩ and \(\langle \bar{1}10\rangle \) orientations. From the fits of H_R, the magnitude of the magnetic anisotropy fields H_A (H_A = H_K, H_B, H_U) for each t_Fe is obtained, and their dependences on inverse Fe thickness \({t}_{\text{Fe}}^{{-}1}\), together with the results obtained from the AlO_x/Fe/GaAs samples, are shown in Extended Data Fig. 2c. The results show that the Pt/Al/Fe/GaAs samples have virtually identical magnetic anisotropies as the AlO_x/Fe/GaAs samples, and introducing the Pt/Al layer neither enhances the magnetization leading to an increase in H_K nor generates a perpendicular anisotropy leading to a decrease in H_K. By comparing the values of H_K and M, we confirm that the main contribution to H_K stems from the magnetization due to the demagnetization field. For both sample series, H_K and H_B decrease as t_Fe decreases because of the reduction of the magnetization as t_Fe decreases, and both of them scale linearly with \({t}_{\text{Fe}}^{{-}1}\). The intercept (about 2,220 mT) of the \({H}_{{\rm{K}}}-{t}_{\text{Fe}}^{-1}\) trace corresponds to the saturation magnetization of bulk Fe, and the intercept (around 45 mT) of the \({H}_{{\rm{B}}}-{t}_{\text{Fe}}^{-1}\) trace corresponds to the biaxial anisotropy of bulk Fe. In contrast to H_K and H_B, H_U shows a linear dependence on \({t}_{\text{Fe}}^{{-}1}\) with a zero intercept, indicative of the interfacial origin of H_U.

Effective mixing conductance in Pt/Al/Fe/GaAs multilayers

Extended Data Fig. 3a,b shows the φ_H dependence and f dependence, respectively, of linewidth ΔH for t_Fe = 1.2 nm. The magnitude of ΔH varies strongly with φ_H because of the presence of in-plane anisotropy, and the dependencies of ΔH on f along both EA and HA show linear behaviour. Both the angular and frequency dependence of ΔH can be well fitted by⁵¹

where Δ[Im(χ)] is the linewidth of the imaginary part of the dynamic magnetic susceptibility Im(χ), H₁ and H₂ are defined in equation (5) for arbitrary H values, and ΔH₀ is the residual linewidth (zero-frequency intercept). As the angular trace can be well fitted by using a damping value of 0.0078, there is no need to consider other extrinsic effects (that is, inhomogeneity and/or two-magnon scattering) contributing to ΔH. It is worth mentioning that the angular trace gives a slightly higher α value because ΔH₀, which also depends on φ_H, is not considered in the fit. In this case, the frequency dependence of linewidth gives more reliable damping values (Extended Data Fig. 3b). Extended Data Fig. 3c compares the magnitude of damping for Pt/Al/Fe/GaAs and AlO_x/Fe/GaAs samples. For both sample series, the Gilbert damping increases as t_Fe decreases and a linear dependence of α on \({t}_{\text{Fe}}^{{-}1}\) is observed. The enhancement of α is because of the spin pumping effect, which is given by^52,53

where α₀ is the intrinsic damping of pure bulk Fe and \({g}_{{\rm{eff}}}^{\uparrow \downarrow }\) is the effective spin mixing conductance quantifying the spin pumping efficiency. By using μ₀M = 2.2 T and γ = 1.80 × 10¹¹ rad s^−1 T^−1, the magnitude of \({g}_{{\rm{eff}}}^{\uparrow \downarrow }\) for Pt/Al/Fe/GaAs is determined to be 4.6 × 10¹⁸ m^−2, and \({g}_{{\rm{eff}}}^{\uparrow \downarrow }\) at the Fe/GaAs interface is determined to be 1.9 × 10¹⁸ m^−2. Therefore, by subtracting these two values, the magnitude of \({g}_{{\rm{eff}}}^{\uparrow \downarrow }\) at Pt/Al/Fe interface is determined to be 2.7 × 10¹⁸ m^−2. The spin transparency T_int of the Pt/Al/Fe interface is given by ref. ⁵³

where 2e²/h is the conductance quantum, G_Pt [= 1/(ρ_xxλ_s)] is the spin conductance of Pt, ρ_xx is the resistivity and λ_s is the spin diffusion length. By using λ_s = 4 nm and an averaged ρ_xx = 40 μΩ cm, T_int = 0.21 is determined. We note that the magnitude of \({g}_{{\rm{eff}}}^{\uparrow \downarrow }\) at the Pt/Al/Fe interface is about one order of magnitude smaller than the experimental values found at heavy metal/ultrathin ferromagnet interfaces⁵⁴, but very close to the value obtained by the first-principles calculations⁵⁵. The previously overestimated \({g}_{{\rm{eff}}}^{\uparrow \downarrow }\) and thus T_int at heavy metal/ultrathin ferromagnet interfaces is probably because the enhancement of α by two-magnon scattering⁵⁶ as well as by the magnetic proximity effect (see Supplementary Note 3) is not properly excluded. Moreover, the obtained α₀ values for Pt/Al/Fe/GaAs (α₀ = 0.0039) and AlO_x/Fe/GaAs (α₀ = 0.0033) slightly differ; the reason is unclear to us, but might be because of a small error in the Fe thickness, which is hard to be determined accurately in the ultrathin regime.

Theory of the modulation of the linewidth

To model the modulation of the FMR linewidth by the application of d.c. current, the Landau–Lifshitz–Gilbert equation with damping-like spin-torque term is considered^18,35,

The terms on the right side of equation (10) correspond to the precession torque, the damping torque and the damping-like spin torque induced by the spin current. Here σ is the spin polarization unit vector, and h_DL is the effective anti-damping-like magnetic field. The effective magnetic field H_eff, containing both external and internal fields, is expressed in terms of the free energy density F, which can be obtained as

For single-crystalline Fe films grown on GaAs(001) substrates with in-plane magnetic anisotropies, F is given by^34,58

Bringing equations (11) and (12) into equation (10), the time-resolved magnetization dynamics for current flowing along the [110] orientation (that is, σ âˆ¥â€‰\([\bar{1}10]\)) is obtained as

Similarly, for the current flowing along the [100]-orientation (that is, σ âˆ¥â€‰[010]), we have

The time dependence of φ(t), θ(t) and then m(t) can be readily obtained from equations (13) and (14), and Extended Data Fig. 4a shows an example of the time-dependent m_z by using μ₀H = 101 mT, μ₀H_K = 1,350 mT, μ₀H_U = 128 mT, μ₀H_B = 10 mT, α = 0.0063 and μ₀H_DL = 0. The damped oscillating dynamic magnetization can be well fitted by

where A is the amplitude, τ is the magnetization relaxation time and ϕ is the phase shift. The connection between τ and ΔH is given by

where dH_R/df can be readily obtained from equation (5). We confirm the validity of the above method in Extended Data Fig. 4b by showing that the angle dependence of ΔH obtained from the time domain (equation (16)) at h_DL = 0 is identical to the linewidth obtained by the dynamic susceptibility in the magnetic field domain (equation (7)).

Having obtained the linewidth for I = 0, the next step is to calculate the influence of the linewidth by spin–orbit torque. The magnitude of h_DL is given by

where ξ is the effective damping-like torque efficiency and j_Pt is the current density in Pt. For the Pt/Al/Fe multilayer, j_Pt is determined by the parallel resistor model

where ρ_Pt (= 40 μΩ cm), ρ_Al (= 10 μΩ cm) and ρ_Fe (= 50 μΩ cm) are the resistivities of the Pt, Al and Fe layers, respectively; t_Pt, t_Al and t_Fe are the thicknesses of the Pt, Al and Fe layers, respectively; I is the d.c. current; and w is the width of the device. Plugging equations (17) and (18) into equations (13) and (14), the I dependence of ΔH can be obtained. An example is shown in Extended Data Fig. 4c, which shows a linear ΔH−I relationship. From the linear fit (equation (1) in the main text), we obtain the modulation amplitude of ΔH, that is, d(ΔH)/dI. Extended Data Fig. 4d presents the calculated d(ΔH)/dI as a function of the magnetic field angle, which shows a strong variation around the HA.

To reproduce the experimental data as shown in Fig. 1f in the main text, the magnitude of the magnetic anisotropies and the damping parameter obtained in Extended Data Fig. 3 as well as ξ = 0.06 are used. Note that the distinctive presence of robust UMA at the Fe/GaAs interface significantly alters the angular dependence of d(ΔH)/dI. This deviation is remarkable when compared with the sinφ_I–H dependence of d(ΔH)/dI as observed in polycrystalline samples, such as Pt/Py (refs. ^57,58).

To understand the strong deviation of d(ΔH)/dI around the HA, we plot the in-plane angular dependence of F in Extended Data Fig. 5 for θ = θ_H = 90°, that is,

It shows that, around the HA (approximately ±15°), the magnetic potential barrier completely vanishes and \(\frac{\partial F}{\partial \varphi }=0\) and \(\frac{{\partial }^{2}F}{\partial \varphi } < 0\) hold. This indicates that the net static torques induced by internal and external magnetic fields acting on the magnetization cancel and the magnetization has a large cone angle for precession⁵⁹. Consequently, the magnetization behaves freely with no constraints in the vicinity of the HA, and the low stiffness allows larger d(ΔH)/dI values induced by spin current⁶⁰. If there are no in-plane magnetic anisotropies, the free energy is constant and is independent of the angle, the magnetization always follows the direction of the applied magnetic field and has the same stiffness at each position. Therefore, the modulation shows no deviation around the HA.

Frequency dependence of the linewidth modulation

Extended Data Fig. 6a shows the frequency dependence of the modulation of linewidth d(ΔH)/dI for t_Fe = 2.8 nm and 1.2 nm, in which the current flows along the [100] orientation. For both samples, the modulation changes polarity as the direction of M is changed by 180°. The modulation amplitude increases quasi-linearly with frequency, and the experimental results can be also reproduced by equation (14) using ξ = 0.06, consistent with the angular modulation shown in Fig. 2f. For H along the ⟨110⟩ and \(\langle \bar{1}10\rangle \) orientations, the frequency and the Fe thickness dependence of linewidth modulation is approximately given by²⁴

where φ_I–H = 45°, 135°, 225° and 315° as shown by the inset of each panel in Extended Data Fig. 6. The damping-like torque efficiency can be further quantified by the slope s of f-dependence modulation, that is, \(s=\frac{\text{d}[\text{d}(\Delta H)\,/\,\text{d}I]}{\text{d}f}\). Extended Data Fig. 7 shows the absolute value of s values as a function of \({t}_{\text{Fe}}^{{-}1}\). A linear dependence of |s| on \({t}_{\text{Fe}}^{{-}1}\) is observed, which indicates that the damping-like torque is an interfacial effect, originating from the absorption of spin current generated in Pt (ref. ⁶¹).

Quantifying the modification of the magnetic anisotropies

In this section, we show our procedure to quantify the modulation of magnetic anisotropies by spin currents. According to equation (5), the f dependencies of H_R along the EA (φ_H = φ = 45° and 225°) and the HA (φ_H = φ = 135° and 315°) are given by equation (3). From the angle and frequency dependencies of H_R as shown in Extended Data Fig. 2, μ₀H_K = 1,350 mT, μ₀H_U = 128 mT, μ₀H_B = 10 mT and g = 2.05 are determined for t_Fe = 1.2 nm. Extended Data Fig. 8a shows the H_R dependence of f for μ₀H_K = 1,350 mT (blue solid line) and μ₀H_K + Δμ₀H_K = 1,400 mT (red solid line) along the HA calculated by equation (3). To exaggerate the difference, μ₀ΔH_K of 50 mT is assumed. The shift of the resonance field ΔH_R is obtained as ΔH_R = H_R(H_K) − H_R(H_K + ΔH_K), and the frequency dependence of ΔH_R is plotted in Extended Data Fig. 8b, which shows a linear behaviour with respect to f between 10 GHz and 20 GHz (in the experimental range), that is, ΔH_R = k_Kf. Note that, to simplify the analysis, the zero-frequency intercept is ignored because the magnitude is much smaller than the intercept induced by ΔH_U and ΔH_B. The sign of the slope k_K is the same as that of ΔH_K and its magnitude is proportional to ΔH_K, that is, k_K ∝ ΔH_K. For the EA as shown in Extended Data Fig. 8c,d, the ΔH_R–f relationship induced by ΔH_K remains the same as for the HA, that is, ΔH_R = k_Kf still holds.

Extended Data Fig. 8e shows the H_Rdependence of f for μ₀H_U = 128 mT (blue solid line) and μ₀H_U + μ₀ΔH_U = 178 mT (red solid line) along the HA. As shown in Extended Data Fig. 8f, the shift of the resonance field along the HA is independent of f with a negative intercept, that is, ΔH_R = −ΔH_U. However, for the EA, as shown in Extended Data Fig. 8g,h, the f-dependent ΔH_R can be expressed as ΔH_R = ΔH_U − k_Uf, which has an opposite slope compared with the ΔH_R–f relationships induced by ∆H_K (Extended Data Fig. 8d), that is, k_U ∝ −ΔH_U.

If the modulation is induced by a change in the biaxial anisotropy as shown in Extended Data Fig. 8i–l, ΔH_R along both the HA and EA shows a linear dependence on f, which is expressed as ΔH_R = −ΔH_B + k_Bf, and k_B ∝ ΔH_B holds.

Extended Data Table 1 summarizes the ΔH_R–f relationships both along the EA and HA induced by ΔH_K, ΔH_U and ΔH_B.

As h_Oe/FL generated by the d.c. current also shifts the resonance field along the EA and HA axes by \(\pm \frac{\sqrt{2}}{2}{h}_{\text{Oe}/\text{FL}}\), where plus corresponds to the [110] (EA) and the \([\bar{1}10]\) (HA) directions, and minus corresponds to the \([\bar{1}\bar{1}0]\) (EA) and the \([1\bar{1}0]\) (HA) directions, the total ΔH_R induced by ΔH_K, ΔH_U and ΔH_B along the EA and HA is, respectively, given by equation (4).

Based on equations (4) and (5), the values of ΔH_K, ΔH_U, ΔH_B and h_Oe/FL for t_Fe ≤ 2.2 nm are extracted as follows:

1. 1.

   We consider the results obtained for H  ∥  M ∥ [110] (EA) and H ∥ M/\([1\bar{1}0]\) (HA) as shown in Extended Data Fig. 9a (the same results as shown in Fig. 4 in the main text for I = 1 mA), where the net magnetization is parallel to I. At f = 0, equation (4) is reduced to

   $$\Delta {H}_{\text{R}}^{\text{EA}}(0)=\Delta {H}_{\text{U}}-\Delta {H}_{\text{B}}+\frac{\sqrt{2}}{2}{h}_{\text{Oe}/\text{FL}}=-0.20\,{\rm{mT}}$$

   (21)

   $$\Delta {H}_{\text{R}}^{\text{HA}}(0)=-(\Delta {H}_{\text{U}}+\Delta {H}_{\text{B}})-\frac{\sqrt{2}}{2}{h}_{\text{Oe}/\text{FL}}=-0.32\,{\rm{mT}}.$$

   (22)

   By adding equations (21) and (22), the magnitude of ΔH_B is determined to be 0.26 mT, which corresponds to k_B of 4 × 10^−3 mT GHz^−1 according to equation (3).

2. 2.

   From Extended Data Fig. 9a, the slope along the HA is determined to be k_K + k_B = 0.025 mT GHz^−1. Thus, the magnitude of k_K is determined by k_K = 0.025 mT GHz^−1 − k_B = 0.021 mT GHz^−1, which corresponds to ΔH_K = 2.0 mT according to equation (3).

3. 3.

   As \(\Delta {H}_{\text{R}}^{\text{EA}}\) is frequency independent, this requires that k_U = k_K + k_B = 0.025 mT GHz^−1, which corresponds ΔH_U = 2.5 mT.

4. 4.

   As the magnetization along EA and HA is, respectively, rotated by 180° to the \([\bar{1}\bar{1}0]\) and \([\bar{1}10]\) directions, and the net magnetization is antiparallel to I (Extended Data Fig. 9b), we obtain ΔH_B = −0.26 mT, ΔH_K = −2.0 mT and ΔH_U = −2.5 mT, which are of opposite sign as the results obtained from Extended Data Fig. 9a.

5. 5.

   Finally, bringing the magnitude of ΔH_B and ΔH_U back into equations (21) and (22), \(\frac{\sqrt{2}}{2}{h}_{\text{Oe}/\text{FL}}\) is determined to be −2.24 mT. The negative sign of h_Oe/FL indicates that it is along the \([0\bar{1}0]\) orientation.

Similarly, the corresponding ΔH_B, ΔH_K and ΔH_U values can be determined for t_Fe = 2.2 nm (Extended Data Fig. 10). Extended Data Table 2 summarizes the magnitudes of the magnetic anisotropy modifications as well as the h_Oe/FL values for all the devices. The enhancement of the field-like torque in thinner samples has been observed in other systems and is probably because of the enhanced Bychkov–Rashba spin–orbit interaction^61,62 and/or the orbital angular momentum (orbital Hall effect and orbital Rashba effect) at the ferromagnetic metal/heavy metal interface⁶².

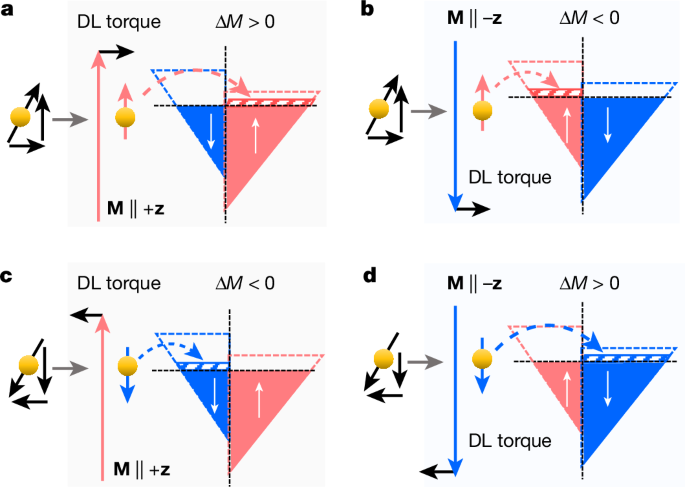
It is worth mentioning that, once the magnetization direction is fixed, ΔH_B, ΔH_K and ΔH_U obtained either from Extended Data Fig. 9a (Extended Data Fig. 10a) or from Extended Data Fig. 9b (Extended Data Fig. 10b) have the same sign (either positive or negative depending on the direction of M). This is consistent with the change in magnetic anisotropies by temperature (Supplementary Fig. 7), which shows that the magnitude of ΔH_B, H_K and ΔH_U increases as the temperature decreases and decreases as the temperature increases. This indicates that the increase in the magnetic anisotropies is dominated by the increase in M as temperature decreases and the decrease in the magnetic anisotropies is dominated by the decrease in M as temperature increases. For the spin current modification demonstrated here, the temperature is not changed but the change in M is induced by populating the electronic bands by the spin current. More interestingly, the new modification method can control the increase or decrease in M simply by the direction of current and/or the direction of magnetization, which is not accessible by other controls.

Alternative interpretation of the experimental results

It is known that the starting point of the FMR analysis is the static magnetic energy landscape, which is related to the magnetic anisotropies. Therefore, it is natural to consider that the modification of magnetic anisotropy accounts for the f-linear dH_R/dI curves as observed in the experiment. Although the data analysis discussed in the previous section is self-consistent, there could be alternative interpretations of the data. One possibility could be the current-induced modification of the Landé g-factor of Fe. In magnetic materials, it is known that g is related to the orbital moment μ_L and the spin moment μ_S:

A flow of spin and orbital angular momentum induced by charge current could, respectively, modify the orbital and spin moment of Fe by Δμ_S and Δμ_L, and then a change in the gyromagnetic ratio of Fe is expected. This could, in turn, lead to a shift of FMR resonance fields linearly depending on the frequency. However, if this were the case, an anisotropic modification of g is needed to interpret the data as observed in Extended Data Figs. 9 and 10 (that is, there is sizeable modification along the HA, but no modification along the EA). As we cannot figure out why the modification of g could be anisotropic, we ignore the discussion of the g-factor modification in the main text. We are also open to other possible explanations for the experimental observations.

Estimation of the magnitude of spin transfer electrons

The change in magnetization is attributed to the additional filling of the electronic d-band. The induced filling of the bands in Fe occurs mainly close to the interface and is not homogeneously distributed, as it depends on the spin diffusion length of the spin current in Fe. In other words, the measured modulated magnetic anisotropies are averaged over the whole ferromagnetic film. For simplicity, we neglect the spin current distribution in Fe and assume that it is homogeneously distributed. The spin chemical potential at the interface⁶³ is given by \({u}_{\text{s}}^{0}=2e\lambda \xi E\tanh \left(\frac{{t}_{\text{Pt}}}{2\lambda }\right)\), where e is the elementary charge, λ is the spin diffusion length, E (= j/σ) is the electric field, j is the current density and σ is the conductivity of Pt. The areal spin density n_s transferred into Fe is obtained as \({n}_{\text{s}}={u}_{\text{s}}^{0}\lambda N\) (ref. ¹⁸), where N is the density of states at the Fermi level. Using N = 6 × 10⁴⁸ J^−1 m^−3, λ = 4 nm, ξ = 0.06, σ  = 2.0 × 10⁶ Ω^−1 m^−1, n_s = 4.2 × 10¹²â€‰Î¼_B cm^−2 is obtained for I = 1 mA. As Fe has a bcc structure (lattice constant a = 2.8 Å) with a moment of about 1.0 μ_B for t_Fe = 1.2 nm at room temperature⁶⁴, the areal density of the magnetic moment of Fe n_Fe is determined to be 2.6 × 10¹⁴ μ_B cm^−2. In this case, the filling of the d-band by spin current leads to a change in the magnetic moment of the order of n_s/n_Fe ≈ 0.16%, which agrees with the ratio between ΔH_K and H_K, that is, ΔH_K/H_K ≈ 2.0 mT/ 1 T ≈ 0.2%.