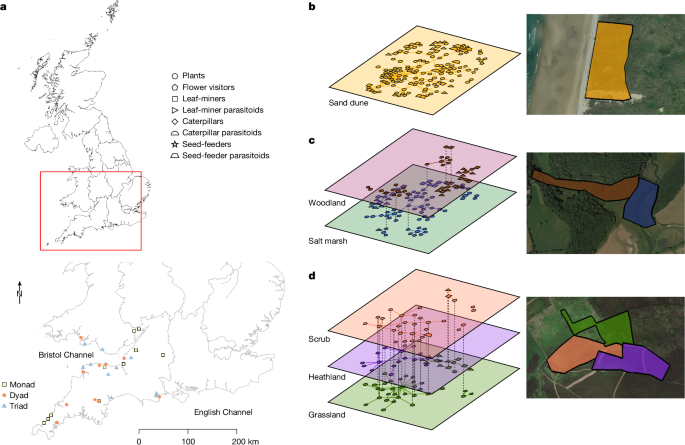
Field sites
We sampled 30 sites in southwest England and southern Wales, each containing one, two or three of six habitat types: woodland, heathland, grassland, salt marsh, sand dunes and scrub. We sampled at ten single-habitat sites, monads, ten two-habitat sites, dyads and ten three-habitat sites, triads. The site size sampled remained constant, thus monads were a single habitat 9âha in size, dyads consisted of two adjacent 4.5âha habitats and triads consisted of three adjacent 3âha habitats. A 9âha field site size was selected to capture the diversity of different taxa across monads, dyads and triads, while also allowing effective sampling of all taxa at each site (plants, herbivores, pollinators and parasitoids). All sites were surrounded by the same habitats as those in the field site or water, urban environment or farmland habitats and each field site was visited once in MayâSeptember 2014 and three times in AprilâSeptember 2015. In 2015, all sites were visited before any site was repeated. In each sampling round, sites were visited in ten three-site cycles, each comprising one monad, dyad and triad. The order of visited sites was randomized within both cycle and round.
Potential sites were initially selected with Arc GIS v.10.1 using the 2007 Land Cover Map32. Three GIS models selected sites that were (1) single-habitat 9âha sites with a 500âm buffer that did not include any other habitat of interest (for example, urban, farmland or water were allowed in the buffer); (2) two 4.5âha contiguous habitats with a 500âm buffer that did not include any other habitat of interest; and (3) three 3âha contiguous habitats with a 500âm buffer that did not include any other habitat of interest. This created a long list of potential sites that were then verified and narrowed down using satellite images (Google Earth 2013) and finally ground-truthed to confirm habitat types, make final selections and outline appropriate habitat plots. The final site list was based on ease of access, travel time, the need to avoid geographic clustering of any site (Fig. 1a) or habitat type, along with our ability to secure permission to sample. We selected habitat combinations such that habitats were represented equally across monads, dyads and triads, while accounting for the restrictions of what was available in the southwest United Kingdom. Because some habitat combinations did not exist in accordance with our selection criteria and others consistently occur together (for example, sand dunes and salt marshes often border grasslands), across monads, dyads and triads, we sampled fewer sand dunes and salt marshes and more grassland and scrub. For a full list of sites see Supplementary Table 3.
Data collection
At each site, on each visit, we sampled along six 35âm transects arranged as follows: six transects in the one monad habitat, three in each dyad habitat and two in each triad habitat. The transect start location and direction were randomly selected before arrival on site and changed on each of the four visits. Thus, in total we sampled along 24 transects at each site.
We designed our data collection under the assumption that sampling intensity is the main driver of speciesâarea relationships, whereas the influence of patch size on per-unit-area (alpha) diversity is weak or absent33,34. Thus, larger patches typically have more species in total because they contain a variety of microhabitats. Repeated sampling across these larger patches would capture more microhabitats and therefore show high between-sample (beta) diversity34. Therefore, to control for these area effects on richness, the sampling effort was consistent at the site level33,34 and thus we standardized the number of samples per site to avoid a patch size bias. Collection protocol closely followed ref. 12 and is described below.
Plant sampling
On each visit, a 0.5âÃâ0.5âm2 gridded quadrat was placed on alternating sides of the transect every 10âm, resulting in four quadrats per transect. All plants were identified and given a vegetation abundance score (as in refs. 12,35). Category 1 species were rare, only present once to a few times (vegetation occupied 1â2% of the quadrat area), category 2 were present in high enough numbers to be seen easily (occupied less than 10% of the quadrat area), category 3 could be seen throughout the quadrat (less than 50% of the area) and category 4 were dominated by the given species (more than 50% of the area). Tree vegetation to a height of 2âm and grasses, the latter collectively pooled, were all classified on this 1â4 scale. All other flowering plant species were identified36 and floral abundance was further classified with buds, open, wilted and seed-set floral units counted. We calculated these per floral unit for flowers arranged in umbels, heads, capitula and spikes. Vegetation cover for flowering species was determined by the number of times a plant touched one of the 36 cross points formed by the intersecting grids on the quadrat. Any plant species that did not fall within a quadrat but which occurred within 30âm of the transect, were recorded but not included in quantitative analysis.
Plantâflower visitor network
On each visit, between 09:00 and 17:30 in dry, warm (minimum 15â°C) conditions with little to no wind, flower visitors were sampled by haphazardly walking for 20âmin, no more than 30âm from the transect. All insects found on a flower head were collected using a hand net. Visited flowers were identified to species in the field and flower visitors were identified to species by taxonomists (see âAcknowledgementsâ).
Plantâherbivoreâparasitoid networks
On each visit, we collected leaf miners and caterpillars from 1âm2 quadrats every 10âm on either side of the transect by visual searching of leaves to a height of 2âm. They were collected and stored individually and returned to the laboratory for rearing.
Leaf miners were initially identified from the leaf mine pattern37,38 and caterpillar species were identified at larval stage39. Individual larvae from both groups were reared in separate pots and checked every 2â3âdays for emergence. Emerged adults, either parasitoid or herbivore, were identified by taxonomists (see Acknowledgements). We used adult identification of surviving individuals to confirm larval identifications, where possible, to ensure accurate identification for herbivores that were either killed by a parasitoid or died during rearing.
Seed herbivores and their parasitoids were collected in seeds in the first and fourth sampling rounds (that is, once in September 2014 and once in AugustâSeptember 2015). Along each transect, we collected up to 50 seeds from plants expected to host seed feeders12,40. Seeds were collected from haphazardly sampled plants within 10âm of the transect and, where possible, from different plants, equally spaced along the transect. Each sample of up to 50 seeds was stored collectively in the same pot and checked weekly until adult herbivores and parasitoids emerged (up to 8âmonths). Each emerged insect, seed feeder or parasitoid, was collected, stored individually and identified by taxonomists. Insects were successfully reared from 23 plant species (Anthyllis vulneraria, Aster tripolium, Centaurea nigra, Cirsium arvense, Cirsium eriophorum, Cirsium palustre, Cirsium vulgare, Crataegus monogyna, Lathyrus pratensis, Lotus corniculatus, Ornithopus perpusillus, Rhinanthus minor, Rosa rugose, Rubus fruticosus agg., Senecio jacobaea, Succisa pratensis, Trifolium arvense, Trifolium pratense, Trifolium repens, Ulex europaeus, Ulex galii, Viccia sativa and Vicia cracca).
Pollination experiment
Between 4 and 14 July 2015, we placed 20 wild strawberry plants (F. vesca) in four 15âl buckets in the centre of each monad and triad; dyads were excluded to allow all plants to be placed and retrieved in the flowering time. Each bucket was surrounded by chicken wire to discourage disturbance by wildlife and livestock (Extended Data Fig. 4). Plants were at the point of flowering when put in the field, then left for 14âdays to allow for natural pollination and then retrieved. It was not possible to collect data on strawberry visitation as the plants could only be left in position for a short period (as seed set occurs relatively quickly) and it was not feasible to simultaneously sample 20 geographically distant field sites (Fig. 1) in a meaningful fashion to record pollinator visitation during this period. F. vesca was selected as it grows naturally in the region, is visited by a wide range of pollinators8 and, although partly wind pollinated, insects are crucial for its successful, uniform pollination21, leading to higher seed set and more symmetrical fruits. Moreover, in commercial varieties, better pollination is linked with increased shelf life and market value13. At the end of the field experiment, we removed all new flower buds and stored the plants in an insect-free greenhouse, watering daily. Strawberries were picked when ripe, weighed and graded according to commercial symmetry ratings41: fruit containing only mild defects in shape (Class I) and those with more severe defects (Class II) (see Extended Data Fig. 5 for example pictures); fruit symmetry significantly affects the market value of commercial strawberries, hence the existence of a grading system. Fruit classes were assigned blindly by an assessor with no knowledge of the field sites, to avoid assessment bias. We stopped fruit collection on greenhouse-stored plants after 28âdays.
Data analysis
Data across all visits were summed to create one network per site with edges weighted by interaction frequency. All analyses were performed and graphs created in the R statistical environment (v.3.6.0)42. All data and code are available at Zenodo (https://doi.org/10.5281/zenodo.11184586)43.
Community structure
We used a MANOVA to test for overall differences in community and network structure among monads, dyads and triads, based on plant species richness, floral abundance, insect species richness, insect abundance, Pielouâs species evenness and interaction evenness, which are expected to change according to land use44. Species evenness was calculated using vegan45 and interaction evenness using bipartite46. To determine the factors contributing to the MANOVA results, we performed pairwise MANOVAs between landscape types and general linear models for each of the six structural aspects (response variables). All residuals were normally distributed and homoscedastic, except for floral abundance, which required a log-transformation: log(xâ+â1).
Community robustness
To determine the response of ecological communities to species extinction, we evaluated the robustness of plantâinsect networks to extinction of plant species from the least to the most common (as in ref. 8). We evaluated how common a plant species is by its average proportion in the landscape; the commonness Cis of plant species i in site s calculated as:
$${C}_{{is}}=\frac{1}{{H}_{s}}\mathop{\sum }\limits_{j=1}^{{H}_{s}}\frac{{a}_{{ij}}}{{A}_{j}}$$
where Hs is the number of habitats in site s, aij/Aj is the proportion of plant species i in habitat j, defining Aj as the total abundance of plant species in habitat j and aij being the abundance of plant species i in habitat j. To calculate this metric for a given plant species, we used its average number of quadrat cross points in each habitat for a given site as a proxy of its local relative abundance.
We modelled a flexible behavioural response of upper trophic levels to their host plantâs extinction. Specifically, the extinction of a plant species can generate cascading loss of species which then allows for rewiring of the network. Herein, we assume that insects are able to reallocate part of their diet on similar resources/hosts, which we determined by identifying the taxa on which species with a similar niche (that is, sharing part of their diet with the focal insect species) feed16. Following ref. 19, we allowed species to reallocate lost interactions to alternative resources/hosts following a primary extinction and probability to interact with a given alternative resource/host was proportional to its abundance (approximated with interaction frequencies). We explored a range of species flexibility, from 0% flexibility (no rewiring allowed) to 100% flexibility (full reallocation of all lost interactions), including intermediate flexibility levels: 25% and 50%. We also explored the range of speciesâ sensitivity to interaction loss, expressed as a percentage of observed feeding interaction events below which a species is considered extinct: 25%, 50% and 75% of lost interactions (all cases are shown in Extended Data Figs. 2 and 3 and robustness to extinctions with full reallocation and 50% sensitivity level is shown in Fig. 3). We extend the approach of ref. 19 to multipartite networks with species interacting at different life stages, by assuming that if one life stage of one species goes extinct (for example, caterpillars), so do the others (for example, the corresponding adult butterfly in the flowerâvisitor network). Thus, species loss can propagate between two types of networks as a result of species being pollinators, herbivores or even parasitoids during different life stages or ecological requirements. Our approach allows rewiring alternatives and species extinction to be evaluated, respectively, for each interaction type and, for each life stage, when applicable.
We repeated this simulation 100 times, both under this scenario and under random removal. Whereas the former tests the response to plant species loss, the latter provides a control scenario accounting for the contribution of basic properties of the networks (size, number of links and so on) to community robustness.
Pollination experiment
The effect of habitat numbers (one or three) on fruit weight and the proportion of Class 1 strawberries (a measure of fruit quality that is determined by pollination success) was assessed using a mixed effect model with site as a random effect and the landscape type (monad or triad) as a fixed effect, using the package lme4 (ref. 47).
Interaction complementarity
Our field experiment supported the idea that pollination function is higher in sites with three habitats than in sites with a single habitat, even if pollinator richness and abundance were similar in sites with different numbers of habitats. Therefore, we asked whether the pollinator communities of sites with more habitats use floral resources in more complementary ways, compared with single-habitat sites, given that there is evidence that interaction complementarity can be associated with increased function23. Our measure of interaction complementarity was adapted from functional diversity analysis methods (for example, refs. 48,49) which measures, for instance, the breadth in species functional traits in ecological communities. Here we measure the breadth of pollinatorsâ use of flower resources; under the assumption that pollinator species with more dissimilar patterns of resource use complement the resource use of other pollinators, thereby increasing pollination function of the community22.
We started by computing the dissimilarity in resource use of pollinators from the plantâpollinator network data. To: (1) have a more complete picture of how complementary pollinator species interactions were in our communities and (2) create a multidimensional functional space which was comparable across sites, we computed a BrayâCurtis dissimilarity matrix from the complete plantâpollinator interaction network, that is all 30 sites pooled together in one interaction network. To control for a potential sampling completeness bias across pollinator species, we normalized pollinator interaction weights, so that interaction weights for each pollinator species summed to 1. We then performed a principal coordinate analysis (PCoA), to place pairwise dissimilarities into a multidimensional space, in which each species is represented by one point and Euclidean distances between species are proportional to their dissimilarities in resource use (Supplementary Fig. 1). We assessed the quality of the functional space using the mean squared deviation index50 and with no obvious break point, selected the space with ten dimensions. Using the FD package51, we then calculated the functional dispersion of each monad and triad site, measured as the sum of the distances of all species in that site to the community centroid. We took this to represent the overall pollinator interaction complementarity at the site level.
Data were normally distributed and had unequal variance, thus we used a Welchâs two sample t-test to determine the difference between the interaction complementarity at monads and triads. Using a linear model, we then tested whether interaction complementarity at each site predicted fruit weight and the proportion of Class 1 strawberries.
Null model tests for additive effects versus emergent properties of several habitats
Using a null model approach27,52, we tested whether the network properties we measured on the sites with several habitats are different from those expected if landscape-scale food webs are simply the sum of their habitats (the null hypothesis). To do so, we first created null triads, that is landscape-scale networks constructed from data collected at monad sites randomly assembled to represent the empirical triad landscapes. Then, we quantified interaction evenness and interaction complementarity for null triads and compared these to empirical triads.
Similar to other measures of biodiversity, network properties are expected to be affected by the size of the sampling area53 as in Supplementary Fig. 2 for three hypothetical habitats: H1, H2 and H3. If landscape-scale food webs are simply the sum of their habitats, then the null hypothesis should translate as follows in terms of species richness and number of interspecific interactions: a triad made of {H1, H2, H3} (each of area Î/3, Î being the area of the sampled site) should have fewer or an equal number of links \({L}_{\left\{{H}_{1},{H}_{2},{H}_{3}\right\},\left\{\varDelta /3,\varDelta /3,\varDelta /3\right\}}\) than the sum of the links in each habitat of size Î/3 (that is, \({L}_{{H}_{1},\varDelta /3}+{L}_{{H}_{2},\varDelta /3}+{L}_{{H}_{3},\varDelta /3}\)). Indeed, a lower number of links would occur if interactions are shared across several habitats. The same rationale applies to the number of species S:
$${S}_{\{{H}_{1},{H}_{2},{H}_{3}\},\{\varDelta /3,\varDelta /3,\varDelta /3\}}\le {S}_{{H}_{1},\varDelta /3}+{S}_{{H}_{2},\varDelta /3}+{S}_{{H}_{3},\varDelta /3}$$
We created two nested null models that generate random plantâinsect interaction networks to test emergent properties within triads.
Null model no. 1. For an observed triad Tk made of {H1, H2, H3}, we created three random networks for each habitat Hi by subsampling the observed monad networks in the corresponding habitats. Thus, a null triad of woodland, heathland and grassland would be created by subsampling the equivalent number of interactions from woodland, heathland and grassland monads. A random network for the habitat Hi in the triad Tk was generated by subsampling \({{N}}_{{{T}}_{{k}},{{H}}_{{i}}}\) (the number of interaction events to consider for the {triad Tk, habitat Hi}-tuple) interactions among those observed in the monad with habitat type Hi (hereafter, monad \({{M}}_{{{H}}_{{i}}}\)). The probability of sampling one interaction was assumed to be proportional to the number of times it had been observed in the monad \({{M}}_{{{H}}_{{i}}}\). For an interaction between species b and species a in monad \({{M}}_{{{H}}_{{i}}}\), this probability is:
$$P((a,b),{M}_{{H}_{i}})={N}_{ab,{M}_{{H}_{i}}}/{N}_{{M}_{{H}_{i}}}$$
where \({{N}}_{{ab},{{M}}_{{{H}}_{{i}}}}\) is the number of individuals of species b recorded interacting with species a in monad \({{M}}_{{{H}}_{{i}}}\) and \({{N}}_{{{M}}_{{{H}}_{{i}}}}\) is the total number of insect individuals seen interacting within monad \({{M}}_{{{H}}_{{i}}}\).
Null model no. 2. In this null model, we also controlled the diversity of the plant community to test whether it contributes to the differences between the observed triads and their random counterparts generated with null model no. 1. To this end, we follow the same steps as for the null model no. 1 but sampled interactions within a subset of monad \({{M}}_{{{H}}_{{i}}}\) involving the same number of plant species as observed interacting in the habitat Hi of the triad Tk.
Evaluating emergent properties
Following the construction of each null triad, we calculated the network properties of interest (interaction evenness and interaction complementarity) and compared them to those of the observed triads. The boxplots in the insets of Fig. 4 and Extended Data Fig. 8 show the range of values for a given network value that we can reasonably expect for a given site under the null hypothesis. If the boxplot overlaps the 1:1 line (that is, xâ=ây line), then the observed value falls within the null hypothesis. If it is below that line, the observed value is less than under the null hypothesis and, if above, more than under the null hypothesis.
Evaluating phylogenetic diversity
To account for the effect of plant phylogenetic diversity in the empirical and simulated triads, we constructed plant phylogenetic trees for each community and measured their phylogenetic diversity as the mean tree branch length. To build one tree per community, we cropped the Daphne phylogeny, a comprehensive dated phylogeny of the European flora54, to only include plant species available in each of our communities. Our visitation dataset contains 149 plant species, out of which 139 species (93%) can be found in the Daphne phylogenetic tree. We standardized synonyms for species that were separately identified using Global Biodiversity Information Facility (GBIF). The remaining ten plant species that are not recorded in the Daphne phylogeny can be divided into two groups as follows (Supplementary Table 1):
-
1.
Plant species that are the only representatives of their genus in our pollination dataset (nâ=â3).
-
2.
Plant species that are not the only representatives of their genus in the dataset (nâ=â7).
These plant species were assigned an alternative replacement species, in their genus, selected from the available species in the phylogeny dataset. The replacements for species in the first group were randomly chosen, as fine-scale phylogenetic distances will probably be less important when a genus is represented by a single species in the data. The replacements for species in the second group were chosen more carefully, as they co-occur with congeneric species, following three steps:
-
(i)
We selected the species from the focal genus available in Daphne phylogeny which were not already part of the interaction dataset.
-
(ii)
In GBIF we obtained the coordinates of the occurrencesâif anyâof these possible species in the United Kingdom.
-
(iii)
For each of the seven species in the second group, we ordered their alternative species from the most to least likely species (measured as number of occurrences in our sampling area). We then selected the top most likely species, which had at least twice as many occurrences as the next likely species. Therefore, the selected species had similarly high occurrences, whereas non-selected species had half or fewer occurrences than the selected species with least occurrences.
If a community included species from the second group and for these species more than one alternative was selected, alternative trees for that community were built and their mean phylogenetic diversity calculated.
We calculated repeated measures correlations between plant phylogenetic diversity and both interaction evenness and interaction complementarity using rmcorr55.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.